题目内容
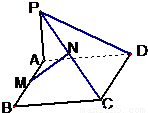
已知PA⊥平面ABCD,且四边形ABCD为矩形,M、N分别是AB、PC的中点.求证:(1)MN∥平面PAD;
(2)MN⊥CD;
(3)当∠PDA=45°,求证:MN⊥平面PCD.
【答案】分析:(1)证明取PD的中点Q,连接NQ,证明NQ∥MA,NQ=MA,从而四边形MNQA为平行四边形,MN∥PQ,再根据直线和平面平行的判定定理证得 MN∥平面PAD.
(2)先证明PA⊥CD,CD⊥AD从而证明CD⊥平面PAD.根据AQ在平面PAD内,可得CD⊥AQ,从而CD⊥MN.
(3)证明:当∠PDA=45°时,△PAD为等腰直角三角形,得到AQ⊥PD,再由CD⊥AQ,可得AQ⊥平面PCD,从而得到 MN⊥平面PCD.
解答:解:(1)证明:∵四边形ABCD为矩形,M、N分别是AB、PC的中点,再取PD的中点Q,连接NQ,
则有NQ∥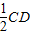 ,且NQ=
,且NQ=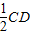 .同理可得 MA∥
.同理可得 MA∥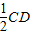 ,且 MA=
,且 MA=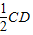 .
.
∴NQ∥MA,NQ=MA. 故四边形MNQA为平行四边形,∴MN∥PQ.
而AQ在平面PAD内,MN不在平面PAD内,∴MN∥平面PAD.
(2)证明:再由PA⊥平面ABCD可得,PA⊥CD,再由四边形ABCD为矩形,可得CD⊥AD.
这样,CD垂直于平面PAD内的两条相交直线,故CD⊥平面PAD. 而AQ在平面PAD内,∴CD⊥AQ,∴CD⊥MN.
(3)证明:当∠PDA=45°时,△PAD为等腰直角三角形,∴AQ⊥PD.
再由CD⊥AQ,可得AQ⊥平面PCD,∴MN⊥平面PCD.
点评:本题考查证明线面平行、线线垂直、线面垂直的方法,直线和平面平行的判定、直线和平面垂直的判定,属于中档题.
(2)先证明PA⊥CD,CD⊥AD从而证明CD⊥平面PAD.根据AQ在平面PAD内,可得CD⊥AQ,从而CD⊥MN.
(3)证明:当∠PDA=45°时,△PAD为等腰直角三角形,得到AQ⊥PD,再由CD⊥AQ,可得AQ⊥平面PCD,从而得到 MN⊥平面PCD.
解答:解:(1)证明:∵四边形ABCD为矩形,M、N分别是AB、PC的中点,再取PD的中点Q,连接NQ,
则有NQ∥
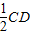 ,且NQ=
,且NQ=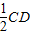 .同理可得 MA∥
.同理可得 MA∥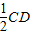 ,且 MA=
,且 MA=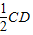 .
.∴NQ∥MA,NQ=MA. 故四边形MNQA为平行四边形,∴MN∥PQ.
而AQ在平面PAD内,MN不在平面PAD内,∴MN∥平面PAD.
(2)证明:再由PA⊥平面ABCD可得,PA⊥CD,再由四边形ABCD为矩形,可得CD⊥AD.
这样,CD垂直于平面PAD内的两条相交直线,故CD⊥平面PAD. 而AQ在平面PAD内,∴CD⊥AQ,∴CD⊥MN.
(3)证明:当∠PDA=45°时,△PAD为等腰直角三角形,∴AQ⊥PD.
再由CD⊥AQ,可得AQ⊥平面PCD,∴MN⊥平面PCD.
点评:本题考查证明线面平行、线线垂直、线面垂直的方法,直线和平面平行的判定、直线和平面垂直的判定,属于中档题.

练习册系列答案
相关题目
 如图,三棱锥P-ABC中,已知PA⊥平面ABC,PA=3,PB=PC=BC=6,求二面角P-BC-A的正弦值.
如图,三棱锥P-ABC中,已知PA⊥平面ABC,PA=3,PB=PC=BC=6,求二面角P-BC-A的正弦值. (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且 (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D,E分别是BC,AP的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D,E分别是BC,AP的中点. (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点. (2013•盐城三模)如图,三棱锥P-ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC中点.
(2013•盐城三模)如图,三棱锥P-ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC中点.