题目内容
过正三棱台的任意两个顶点的直线有15条,其中异面直线有( )对.A.12
B.24
C.36
D.48
【答案】分析:直接解答,先看与下底面上的一条边对应的异面直线的条数,类推到上底面的边;再求侧面上的异面直线的对数即可.
解答:解:正三棱台上底面和下底面各有三条边
各个侧面均为四边形,各有六条线段,
这样每条棱被算了两次,共9条棱
∴共有3×2+3×6-9=15条直线
分三类:
①三棱台的上底面三角形中任意取一条边a,
这样在与a异面的直线一共5条,这样算3条底边
一共有3×5=15对异面直线;
②三棱台的下底面三角形中任意取一条边b,
这样在与b异面的直线一共5条,这样算3条底边
一共有3×5=15对异面直线;
③分别位于两个侧面且不在底面的异面直线:
共(3×4)÷2=6对
综上所述,所有的中异面直线有15+15+6=36对.
故选C.
点评:本题考查棱台的结构特征,异面直线的判断,排列组合的实际应用,是难题.
解答:解:正三棱台上底面和下底面各有三条边
各个侧面均为四边形,各有六条线段,
这样每条棱被算了两次,共9条棱
∴共有3×2+3×6-9=15条直线
分三类:
①三棱台的上底面三角形中任意取一条边a,
这样在与a异面的直线一共5条,这样算3条底边
一共有3×5=15对异面直线;
②三棱台的下底面三角形中任意取一条边b,
这样在与b异面的直线一共5条,这样算3条底边
一共有3×5=15对异面直线;
③分别位于两个侧面且不在底面的异面直线:
共(3×4)÷2=6对
综上所述,所有的中异面直线有15+15+6=36对.
故选C.
点评:本题考查棱台的结构特征,异面直线的判断,排列组合的实际应用,是难题.

练习册系列答案
相关题目
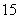 条,其中异面直线有( )对
条,其中异面直线有( )对