题目内容
若S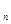 是公差不为0的等差数列
是公差不为0的等差数列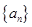 的前
的前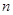 项和,且
项和,且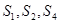 成等比数列。
成等比数列。
(1)求等比数列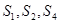 的公比;
的公比;
(2)若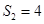 ,求
,求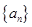 的通项公式;
的通项公式;
(3)设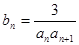 ,
,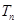 是数列
是数列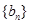 的前
的前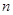 项和,求使得
项和,求使得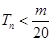 对所有
对所有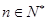 都成立的最小正整数
都成立的最小正整数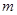 。
。
【答案】
(1) 4(2) 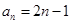 (3) 30
(3) 30
【解析】
试题分析:∵数列{an}为等差数列,∴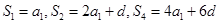 ,
,
∵S1,S2,S4成等比数列,∴ S1·S4
=S22 ∴  ,∴
,∴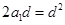
∵公差d不等于0,∴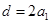
(1)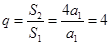 (2)∵S2 =4,∴
(2)∵S2 =4,∴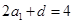 ,又
,又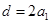 ,
,
∴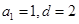 , ∴
, ∴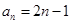 。
。
(3)∵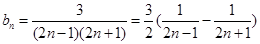
∴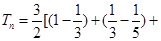 …
…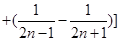
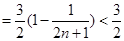
要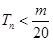 n∈N*恒成立,∴
n∈N*恒成立,∴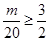 ,
,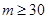 ,∵m∈N* ∴m的最小值为30。
,∵m∈N* ∴m的最小值为30。
考点:等差数列等比数列及数列求和
点评:等差数列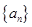 中,首项
中,首项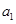 ,公差
,公差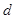 则通项为
则通项为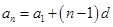 ,若
,若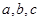 成等比数列,则
成等比数列,则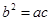 ,第三问的数列求和中用到了裂项相消的方法,此方法一般适用于通项公式为
,第三问的数列求和中用到了裂项相消的方法,此方法一般适用于通项公式为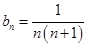 形式的数列求和
形式的数列求和

练习册系列答案
相关题目
 是公差不为0的等差数列
是公差不为0的等差数列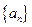 的前n项和,且
的前n项和,且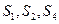 成等比数列。
成等比数列。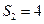 ,求
,求 ,
,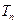 是数列
是数列 的前n项和,求使得
的前n项和,求使得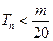 对所有
对所有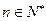 都成立的最小正整数m。
都成立的最小正整数m。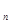 是公差不为0的等差数列
是公差不为0的等差数列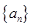 的前n项和,且
的前n项和,且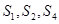 成等比数列。
成等比数列。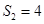 ,求
,求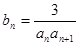 ,
,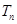 是数列
是数列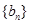 的前n项和,求使得
的前n项和,求使得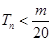 对所有
对所有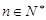 都成立的最小正整数
都成立的最小正整数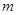 。
。