题目内容
如果正三棱锥的侧面均为直角三角形,侧面与底面所成的角为α,则α的值是
arcos
| ||
| 3 |
arcos
.
| ||
| 3 |
分析:根据所给的正三棱锥的特点,根据三垂线定理做出二面角的平面角,在直角三角形中做出要用的两条边的长度,根据三角函数的定义得到角的余弦值,得到角.
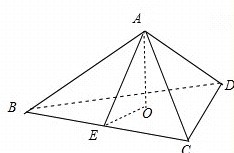
解答:解:过A做地面的垂线AO,在面ABC上,做BC的垂线AE,连接EO,
则∠AEO就是要求的二面角的平面角,
设侧棱长是1,在等腰直角三角形中AE=
BC=
,
EO=
DE=
×
=
,
∴cosα=
=
,
∴α=arccos
故答案为:arccos
则∠AEO就是要求的二面角的平面角,
设侧棱长是1,在等腰直角三角形中AE=
| 1 |
| 2 |
| ||
| 2 |

EO=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| ||
| 2 |
| ||
| 6 |
∴cosα=
| ||||
|
| ||
| 3 |
∴α=arccos
| ||
| 3 |
故答案为:arccos
| ||
| 3 |
点评:本题看出二面角的平面角及其求法,本题解题的关键是做出二面角的平面角,把角放到一个可解的直角三角形中来做出结果,本题是一个中档题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目