题目内容
设f(k)是满足不等式log2x+log2(3·2k-1-x)≥2k-1(k∈N)的自然数的个数.(1)求f(k)的解析式;
(2)记Sn=f(1)+f(2)+f(3)+…+f(n),求Sn的解析式;
(3)令Pn=n2+n-1(n∈N*),试比较Sn与Pn的大小.
解:先由条件解关于x的不等式,从而求出f(k).
(1)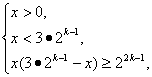
即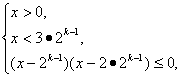
∴2k-1≤x≤2k.当k=0时,![]() ≤x≤1,∴f(k)=1.当k∈N*时,f(k)=2k-2k-1+1=2k-1+1.
≤x≤1,∴f(k)=1.当k∈N*时,f(k)=2k-2k-1+1=2k-1+1.
∴f(k)=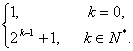
(2)Sn=f(1)+f(2)+…+f(n)=20+21+…+2n-1+n=2n+n-1.
(3)Sn-Pn=2n-n2,
当n=1时,21-12>0;
当n=2时,22-22=0;
当n=3时,23-32<0;
当n=4时,24-42=0;
当n=5时,25-52>0.
猜想:n≥5时,Sn>Pn.
下面用数学归纳法证明:
①当n=5时,25>52.
②假设n=k(k≥5)时,Sn>Pn,即2k>k2,
那么2k+1=2·2k>2k2=k2+2k+1+k2-2k-1=(k+1)2+[k(k-2)-1].
∵k≥5,∴k(k-2)-1>0.
∴(k+1)2+[k(k-2)-1]>0,
即2k+1>(k+1)2.∴当n=k+1时,Sn>Pn.
由①②知n∈N,n≥5时,Sn>Pn.
综上,n=1或n≥5时,Sn>Pn;
n=2或n=4时,Sn=Pn;n=3时,Sn<Pn.

练习册系列答案
相关题目
 是递增闭函数,则实数k的取值范围是( )
是递增闭函数,则实数k的取值范围是( )