题目内容
正三棱台的上、下底边长为2和4．（Ⅰ）若该正三棱台的高为 1，求此三棱台的侧面积；
（Ⅱ）若侧面与底面所成的角是60°，求此三棱台的体积；
参考公式：台体的体积公式V台体=
| 1 |
| 3 |
| SS′ |
分析：（Ⅰ）取A1B1，AB中点D1，DO1，O分别为△A1B1C1，△ABC的中心，过D1作D1M⊥DC，利用三棱台的侧面积公式，即可求得结论；
（Ⅱ）确定台体的高，再确定上、下底的面积，即可求此三棱台的体积．
（Ⅱ）确定台体的高，再确定上、下底的面积，即可求此三棱台的体积．
解答：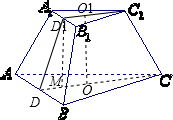
解：（Ⅰ）取A1B1，AB中点D1，D，O1，O分别为△A1B1C1，△ABC的中心，过D1作D1M⊥DC，则D1C1=
，DC=2
从而D1O1=
，DO=
，∴DM=
，
∵D1M=1，∴D1D=
∴S侧=3×
=6
（Ⅱ）由（Ⅰ）知，在直角△D1DM中，∠D1DM=60°，即侧面与底面所成的角，故台体的高为1，
∵正三棱台的上、下底边长为2和4
∴S△A1B1C1=
，S△ABC=4
∴V台=
×1×(
+
+4
)=
解：（Ⅰ）取A1B1，AB中点D1，D，O1，O分别为△A1B1C1，△ABC的中心，过D1作D1M⊥DC，则D1C1=| 3 |
| 3 |
从而D1O1=
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
∵D1M=1，∴D1D=
2
| ||
| 3 |
∴S侧=3×
(2+4)×
| ||||
| 2 |
| 3 |
（Ⅱ）由（Ⅰ）知，在直角△D1DM中，∠D1DM=60°，即侧面与底面所成的角，故台体的高为1，
∵正三棱台的上、下底边长为2和4
∴S△A1B1C1=
| 3 |
| 3 |
∴V台=
| 1 |
| 3 |
| 3 |
|
| 3 |
7
| ||
| 3 |
点评：本题考查求此三棱台的侧面积、体积，考查学生的计算能力，属于中档题．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
正三棱台的上、下底边长为2和4．
的上、下底边长之比为2∶3，连结
及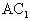
，把正三棱台分成三个三棱锥，则这三个三棱锥体积之比(由小到大)是________．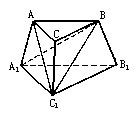
．