题目内容
点Q位于直线x=-3右侧,且到点F(-1,0)与到直线x=-3的距离之和等于4.(1)求动点Q的轨迹C;
(2)直线l过点M(1,0)交曲线C于A、B两点,点P满足
| FP |
| 1 |
| 2 |
| FA |
| FB) |
| EP |
| AB |
| OE |
(3)在(2)的条件下,△PEF能否成为以EF为底的等腰三角形?若能,求出此时直线l的方程;若不能,请说明理由.
分析:(1)由于题设条件中知Q位于直线x=-3右侧,且到点F(-1,0)与到直线x=-3的距离之和等于4,故可设出Q(x,y),利用距离之和等于建立方程,整理出动点Q的轨迹C的方程;
(2)先处理条件点P满足
=
(
+
,
•
=0,又
=(x0,0),得出P是AB中点,E是线段AB垂直平分线与X轴交点,设出直线l的方程为y=k(x-1),代入轨迹C的方程得到:k2x2+(4-2k2)x+k2=0(-3<x≤0)(*)找出l与C有两个不同交点的条件
,解出引入的参数k的取值范围,再由根与系数的关系解出AB中点P的坐标(用k表示),得出直线EP的方程,再研究E点的横坐标求出x0的取值范围;
(3)不妨先假设可以,则须有2xP=xE+xF,即:2(1-
)=-1-
-1,解得:k2=
,这与(2)中的条件矛盾,即可说明这样的直线不存在
(2)先处理条件点P满足
| FP |
| 1 |
| 2 |
| FA |
| FB) |
| EP |
| AB |
| OE |
|
(3)不妨先假设可以,则须有2xP=xE+xF,即:2(1-
| 2 |
| k2 |
| 2 |
| k2 |
| 1 |
| 2 |
解答:解:(1)Q(x,y),则|QF|+x+3=4(x>-3),即:
+x+3=4(x>-3),化简得:y2=-4x(-3<x≤0).
所以,动点Q的轨迹为抛物线y2=-4x位于直线x=-3右侧的部分.…(4分)
(2)因为
=
(
+
,所以,P为AB中点;又因为
•
=0,且
=(x0,0),所以,点E为线段AB垂直平分线与x轴交点.
由题可知:直线l与x轴不垂直,所以可设直线l的方程为y=k(x-1),代入轨迹C的方程得到:k2x2+(4-2k2)x+k2=0(-3<x≤0)(*)
设f(x)=k2x2+(4-2k2)x+k2,要使得l与C有两个不同交点,需且只需
解之得:
<k2<1.
由(*)式得:xA+xB=
,所以,AB中点P的坐标为:xP=
=1-
,yP=k(xF-1)=-
.
所以,直线EP的方程为y+
=-
(x-1+
)
令y=0得到点E的横坐标为xE=-1-
.
因为
<k2<1,所以,xE∈(-
,-3).…(10分)
(3)不可能.…(11分)
要使△PEF成为以EF为底的等腰三角形,需且只需2xP=xE+xF,即:2(1-
)=-1-
-1,解得:k2=
.
另一方面,要使直线l满足(2)的条件,需要
<k2<1,所以,不可能使△PEF成为以EF为底的等腰三角形.…(14分)
| (x+1)2+y2 |
所以,动点Q的轨迹为抛物线y2=-4x位于直线x=-3右侧的部分.…(4分)
(2)因为
| FP |
| 1 |
| 2 |
| FA |
| FB) |
| EP |
| AB |
| OE |
由题可知:直线l与x轴不垂直,所以可设直线l的方程为y=k(x-1),代入轨迹C的方程得到:k2x2+(4-2k2)x+k2=0(-3<x≤0)(*)
设f(x)=k2x2+(4-2k2)x+k2,要使得l与C有两个不同交点,需且只需
|
解之得:
| 3 |
| 4 |
由(*)式得:xA+xB=
| 2k2-4 |
| k2 |
| xA+xB |
| 2 |
| 2 |
| k2 |
| 2 |
| k |
所以,直线EP的方程为y+
| 2 |
| k |
| 1 |
| k |
| 2 |
| k2 |
令y=0得到点E的横坐标为xE=-1-
| 2 |
| k2 |
因为
| 3 |
| 4 |
| 11 |
| 3 |
(3)不可能.…(11分)
要使△PEF成为以EF为底的等腰三角形,需且只需2xP=xE+xF,即:2(1-
| 2 |
| k2 |
| 2 |
| k2 |
| 1 |
| 2 |
另一方面,要使直线l满足(2)的条件,需要
| 3 |
| 4 |
点评:本题考查求轨迹方程,解题的关键是理解题意,由题设中所给的等量关系建立方程求出轨迹方程,本题第二小题的求解要注意位置关系与方程的转化,由此得出两曲线有两个交点的条件,从而研究出点的横坐标的取值范围,本题中第三小题的求解用到了反证法的思想,先假设问题成立,由此出发推出矛盾,本题综合性强,转化灵活,涉及到的知识方法较多,解题时要注意体会总结知识的用法技巧与转化技巧,本题易因为不知怎么转化而导致无法解题

练习册系列答案
相关题目
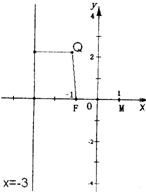 已知点Q位于直线x=-3右侧,且到点F(-1,0)与到直线x=-3的距离之和等于4.
已知点Q位于直线x=-3右侧,且到点F(-1,0)与到直线x=-3的距离之和等于4.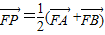 ,
,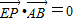 ,又
,又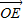 =(x,0),其中O为坐标原点,求x的取值范围;
=(x,0),其中O为坐标原点,求x的取值范围;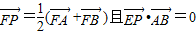 ,其中点E的坐标为(x,0),试求x的取值范围.
,其中点E的坐标为(x,0),试求x的取值范围.