题目内容
已知函数f(x)=sin  ·sin
·sin  +
+ sin xcos x(x∈R).
sin xcos x(x∈R).
(1)求f 的值;
的值;
(2)在△ABC中,若f =1,求sin B+sin C的最大值.
=1,求sin B+sin C的最大值.
 ·sin
·sin  +
+ sin xcos x(x∈R).
sin xcos x(x∈R).(1)求f
 的值;
的值;(2)在△ABC中,若f
 =1,求sin B+sin C的最大值.
=1,求sin B+sin C的最大值.(1)1(2)

(1)f(x)=sin sin
sin +
+ sin xcos x=
sin xcos x=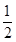 cos 2x+
cos 2x+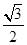 sin 2x=sin
sin 2x=sin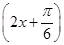 ,所以f
,所以f =1.
=1.
(2)由f =1,有f
=1,有f =sin
=sin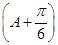 =1,因为0<A<π,所以A+
=1,因为0<A<π,所以A+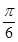 =
=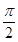 ,即A=
,即A=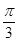 .
.
sin B+sin C=sin B+sin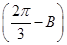 =
= sin B+
sin B+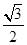 cos B=
cos B= sin
sin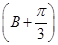 .
.
因为0<B<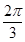 ,所以
,所以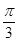 <B+
<B+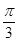 <π,0<sin
<π,0<sin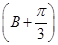 ≤1,
≤1,
所以sin B+sin C的最大值为 .
.
 sin
sin +
+ sin xcos x=
sin xcos x=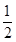 cos 2x+
cos 2x+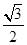 sin 2x=sin
sin 2x=sin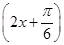 ,所以f
,所以f =1.
=1.(2)由f
 =1,有f
=1,有f =sin
=sin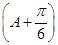 =1,因为0<A<π,所以A+
=1,因为0<A<π,所以A+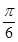 =
=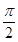 ,即A=
,即A=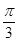 .
.sin B+sin C=sin B+sin
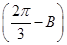 =
= sin B+
sin B+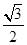 cos B=
cos B= sin
sin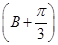 .
.因为0<B<
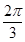 ,所以
,所以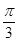 <B+
<B+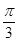 <π,0<sin
<π,0<sin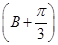 ≤1,
≤1,所以sin B+sin C的最大值为
 .
.
练习册系列答案
相关题目
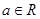 函数
函数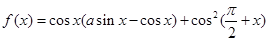 满足
满足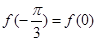 .
.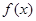 的单调递减区间;
的单调递减区间;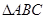 的内角
的内角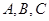 所对的边分别为
所对的边分别为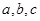 ,且
,且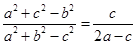 ,求
,求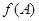 的取值范围.
的取值范围. ,cos(α-β)=
,cos(α-β)= ,且0<β<α<
,且0<β<α< ,求β.
,求β.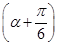 =
=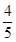 ,则sin
,则sin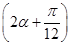 的值为________.
的值为________.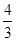 ,sin(α+β)=
,sin(α+β)=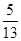 ,其中α,β∈(0,π),则sin α的值为( ).
,其中α,β∈(0,π),则sin α的值为( ).


 的值为 ( ).
的值为 ( ).


 =( )
=( )  ( )
( )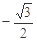



 的值( )
的值( )


