题目内容
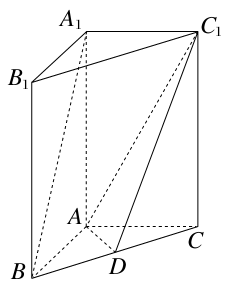
如图, 和
和 所在平面互相垂直,且
所在平面互相垂直,且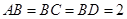 ,
, ,E、F分别为AC、DC的中点.
,E、F分别为AC、DC的中点.
(1)求证: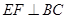 ;
;
(2)求二面角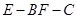 的正弦值.
的正弦值.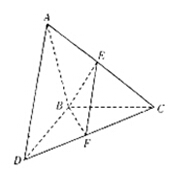
(1)详见解析;(2) 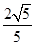 .
.
解析试题分析:(1)(方法一)过E作EO⊥BC,垂足为O,连OF,由△ABC≌△DBC可证出△EOC≌△FOC,所以∠EOC=∠FOC= ,即FO⊥BC,又EO⊥BC,因此BC⊥面EFO,即可证明EF⊥BC.(方法二)由题意,以B为坐标原点,在平面DBC内过B左垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示的空间直角坐标系.
,即FO⊥BC,又EO⊥BC,因此BC⊥面EFO,即可证明EF⊥BC.(方法二)由题意,以B为坐标原点,在平面DBC内过B左垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示的空间直角坐标系.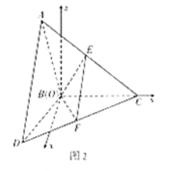
易得 ,所以
,所以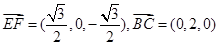 ,因此
,因此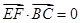 ,从而得
,从而得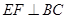 ;(2) (方法一)在图1中,过O作OG⊥BF,垂足为G,连EG,由平面ABC⊥平面BDC,从而EO⊥平面BDC,从而EO⊥面BDC,又OG⊥BF,由三垂线定理知EG垂直BF,因此∠EGO为二面角E-BF-C的平面角;在△EOC中,EO=
;(2) (方法一)在图1中,过O作OG⊥BF,垂足为G,连EG,由平面ABC⊥平面BDC,从而EO⊥平面BDC,从而EO⊥面BDC,又OG⊥BF,由三垂线定理知EG垂直BF,因此∠EGO为二面角E-BF-C的平面角;在△EOC中,EO= EC=
EC= BC·cos30°=
BC·cos30°=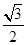 ,由△BGO∽△BFC知,
,由△BGO∽△BFC知,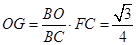 ,因此tan∠EGO=
,因此tan∠EGO=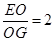 ,从而sin∠EGO=
,从而sin∠EGO=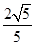 ,即可求出二面角E-BF-C的正弦值.
,即可求出二面角E-BF-C的正弦值.
(方法二)在图2中,平面BFC的一个法向量为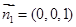 ,设平面BEF的法向量
,设平面BEF的法向量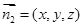 ,又,由
,又,由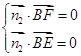 得其中一个
得其中一个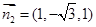 ,设二面角E-BF-C的大小为
,设二面角E-BF-C的大小为 ,且由题意知
,且由题意知 为锐角,则
为锐角,则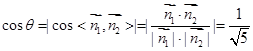 ,因此sin∠EGO=
,因此sin∠EGO=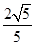 ,即可求出二面角E-BF-C的正弦值.
,即可求出二面角E-BF-C的正弦值.
(1)证明:
(方法一)过E作EO⊥BC,垂足为O,连OF,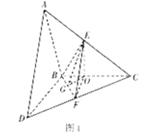
由△ABC≌△DBC可证出△EOC≌△FOC,所以∠EOC=∠FOC= ,即FO⊥BC,
,即FO⊥BC,
又EO⊥BC,因此BC⊥面EFO,
又EF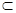 面EFO,所以EF⊥BC.
面EFO,所以EF⊥BC.
(方法二)由题意,以B为坐标原点,在平面DBC内过B左垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示的空间直角坐标系.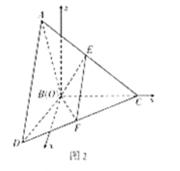
易得B(0,0,0),A(0,-1, ),D(
),D( ,-1,0),C(0,2,0),因而
,-1,0),C(0,2,0),因而 ,所以
,所以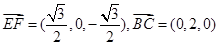 ,因此
,因此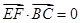 ,从而
,从而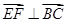 ,所以
,所以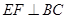 .
.
(2)(方法一)在图1中,过O作OG⊥BF,垂足为G,连EG,由平面ABC⊥平面BDC,从而EO⊥平面BDC,从而EO⊥面BDC,又OG⊥BF,由三垂线定理知EG垂直BF.
因此∠EGO为二面角E-BF-C的平面角;
在△EOC中,EO= EC=
EC= BC·cos30°=
BC·cos30°=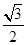 ,由△BGO∽△BFC知,
,由△BGO∽△BFC知,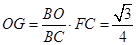 ,因此tan∠EGO=
,因此tan∠EGO=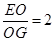 ,从而sin∠EGO=
,从而sin∠EGO=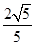 ,即二面角E-BF-C的正弦值为
,即二面角E-BF-C的正弦值为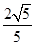 .
.
(方法二)在图2中,平面BFC的一个法向量为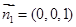 ,设平面BEF的法向量
,设平面BEF的法向量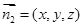 ,又
,又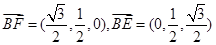 ,由
,由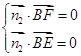 得其中一个
得其中一个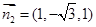 ,设二面角E-BF-C的大小为
,设二面角E-BF-C的大小为 ,且由题意知
,且由题意知 为锐角,则
为锐角,则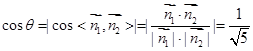 ,因此sin∠EGO=
,因此sin∠EGO=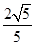 ,即二面角E-BF-C的正弦值为
,即二面角E-BF-C的正弦值为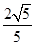 .
.
考点:1.线面垂直的判定;2.二面角.

 名校课堂系列答案
名校课堂系列答案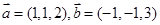 ,且
,且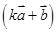 //(
//(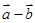 ),则k=______.
),则k=______. ,则点
,则点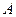 关于
关于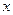 轴对称的点的坐标为 。
轴对称的点的坐标为 。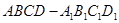 中,
中,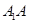
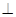 底面
底面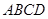 .四边形
.四边形 ,且
,且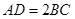 .过
.过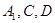 三点的平面记为
三点的平面记为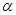 ,
,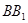 与
与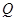 .
.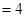 ,
,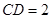 ,梯形
,梯形
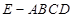 中,平面
中,平面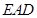
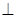 平面
平面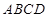 ,
,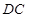 //
//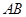 ,
,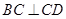 ,
,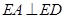 ,且
,且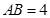 ,
,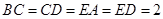 .
.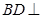 平面
平面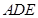 ;
;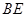 和平面
和平面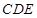 所成角的正弦值;
所成角的正弦值; 上是否存在一点
上是否存在一点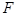 使得平面
使得平面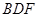
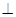 平面
平面
 的正方形
的正方形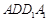 中,点
中,点 在线段
在线段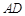 上,且
上,且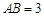 ,
,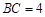 ,作
,作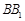 //
//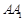 ,分别交
,分别交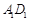 ,
,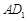 于点
于点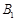 ,
,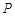 ,作
,作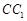 //
//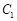 ,
,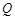 ,将该正方形沿
,将该正方形沿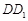 与
与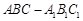 .
.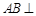 平面
平面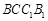 ;
; 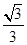 ,求|BE|的最小值.
,求|BE|的最小值.
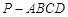 中,
中,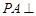 平面
平面 ,
,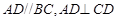 ,且
,且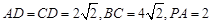 ,点
,点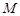 在
在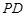 上.
上.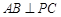 ;
;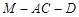 的大小为
的大小为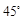 ,求
,求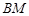 与平面
与平面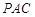 所成角的正弦值.
所成角的正弦值.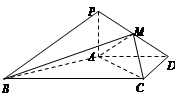
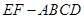 中,
中,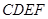 为边长为
为边长为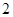 的正方形,
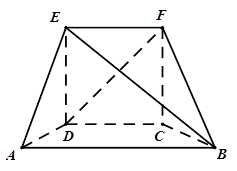
的正方形,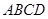 为直角梯形,
为直角梯形,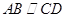 ,
,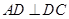 ,
,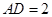 ,
,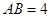 ,
,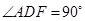 .
.
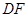 和
和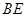 所成角的大小;
所成角的大小;