题目内容
已知函数F(x)=- x4+ax3+
x4+ax3+ x2+b,(a,b为常数),
x2+b,(a,b为常数),
(1)当a=1时,F(x)=0有两个不相等的实根,求b的取值范围;
(2)若F(x)有三个不同的极值点0、x1、x2,a为何值时,能使函数F(x)在x1(或x2)处取得的极值为b?
(3)若对任意的a∈[-1,0],不等式F(x)≥-8在[-2,2]上恒成立,求b的取值范围.
 x4+ax3+
x4+ax3+ x2+b,(a,b为常数),
x2+b,(a,b为常数),(1)当a=1时,F(x)=0有两个不相等的实根,求b的取值范围;
(2)若F(x)有三个不同的极值点0、x1、x2,a为何值时,能使函数F(x)在x1(或x2)处取得的极值为b?
(3)若对任意的a∈[-1,0],不等式F(x)≥-8在[-2,2]上恒成立,求b的取值范围.
解:(1)当a=1时, ,
,
记 ,
,
则 ,
,
令g′(x)=0,得x=-1,0,4,
当x变化时,g′(x)、g(x)的变化情况如下表:

由已知,知直线y=b与y=g(x)的图象有且只有两个公共点,所以 或b>0,
或b>0,
∴b的取值范围为 。
。
(2) ,
,
则 是
是 的两个不相等的非零实根,
的两个不相等的非零实根,
∴ ,且
,且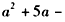
 ,(*)
,(*)
不妨设 ,
,
∴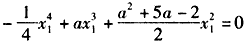 ,
,
即 ,①,
,①,
又∵ ,②
,②
①+②,得 ,即
,即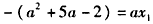 ,③
,③
代入②,得x12-2ax1=0,
∵x1≠0,∴x1=2a,
代入③,得 ,
,
∴a=-2或 ,经检验,a=-2或
,经检验,a=-2或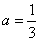 都满足(*),
都满足(*),
故a=-2或 。
。
(3)当a∈[-1,0]时,可知 ,
,
∴ 恒成立,
恒成立,
∴x>0时,f′(x)<0;x<0时,f′(x)>0,
∴F(x)在(-∞,0)内递增,在(0,+∞)内递减,
∴F(x)在[-2,2]上的最小值min{F(-2),F(2)}=2a2+18a-8+b≥-8恒成立,
∴ ,
,
当a=-1时,-2a2-18a取最大值16,
所以b的取值范围为[16,+∞).
 ,
,记
 ,
,则
 ,
,令g′(x)=0,得x=-1,0,4,
当x变化时,g′(x)、g(x)的变化情况如下表:

由已知,知直线y=b与y=g(x)的图象有且只有两个公共点,所以
 或b>0,
或b>0, ∴b的取值范围为
 。
。(2)
 ,
,则
 是
是 的两个不相等的非零实根,
的两个不相等的非零实根,∴
 ,且
,且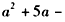
 ,(*)
,(*) 不妨设
 ,
,∴
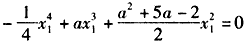 ,
,即
 ,①,
,①,又∵
 ,②
,② ①+②,得
 ,即
,即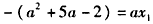 ,③
,③ 代入②,得x12-2ax1=0,
∵x1≠0,∴x1=2a,
代入③,得
 ,
,∴a=-2或
 ,经检验,a=-2或
,经检验,a=-2或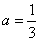 都满足(*),
都满足(*),故a=-2或
 。
。(3)当a∈[-1,0]时,可知
 ,
,∴
 恒成立,
恒成立,∴x>0时,f′(x)<0;x<0时,f′(x)>0,
∴F(x)在(-∞,0)内递增,在(0,+∞)内递减,
∴F(x)在[-2,2]上的最小值min{F(-2),F(2)}=2a2+18a-8+b≥-8恒成立,
∴
 ,
,当a=-1时,-2a2-18a取最大值16,
所以b的取值范围为[16,+∞).

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|