题目内容
已知椭圆C: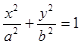
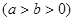 的短轴长等于焦距,椭圆C上的点到右焦点
的短轴长等于焦距,椭圆C上的点到右焦点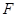 的最短距离为
的最短距离为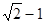 .
.
(1)求椭圆C的方程;
(2)过点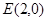 且斜率为
且斜率为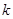 (
(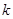 >0)的直线
>0)的直线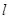 与C交于
与C交于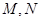 两点,
两点,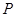 是点
是点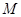 关于
关于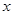 轴的对称点,证明:
轴的对称点,证明: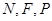 三点共线.
三点共线.
【答案】
(1)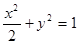 (2)设出直线
(2)设出直线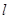 的方程,联立方程组即可利用利用两个向量共线证明三点共线
的方程,联立方程组即可利用利用两个向量共线证明三点共线
【解析】
试题分析:(1)由题意: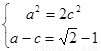 ,得
,得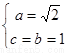
所求椭圆的方程为: 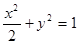 …4分
…4分
(2)设直线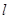 :
: ,
,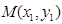 ,
,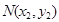 ,
,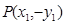 ,
,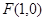 ,
,
由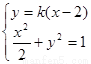 消
消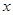 得:
得: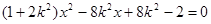

所以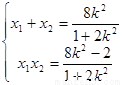 …8分
…8分
而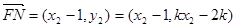 ,
,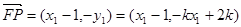
∵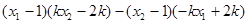 =
= 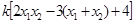
=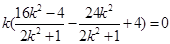 ,
,
∴ 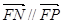 . 又
. 又 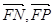 有公共点
有公共点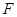 ∴
∴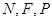 三点共线. …14分
三点共线. …14分
考点:本小题主要考查椭圆方程的求解和向量共线的应用.
点评:证明三点共线,一般转化为两个两个向量共线,而这又离不开直线方程和椭圆方程联立方程组,运算量比较大,要注意“舍而不求”思想的应用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 的短轴长为
的短轴长为 ,且斜率为
,且斜率为 的直线
的直线 过椭圆C的焦点及点
过椭圆C的焦点及点 。
。 过椭圆C的左焦点
过椭圆C的左焦点 ,交椭圆于点P、Q,
,交椭圆于点P、Q, (
( 为坐标原点),求
为坐标原点),求 的面积;
的面积; 轴上,且使
轴上,且使 为
为 的一条角平分线,则称点M为椭圆C的“左特征点”,求椭圆C的左特征点。
的一条角平分线,则称点M为椭圆C的“左特征点”,求椭圆C的左特征点。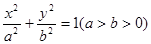 的短轴长为
的短轴长为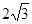 ,右焦点
,右焦点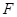 与抛物线
与抛物线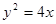 的焦点重合,
的焦点重合, 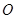 为坐标原点
为坐标原点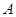 、
、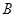 是椭圆C上的不同两点,点
是椭圆C上的不同两点,点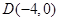 ,且满足
,且满足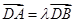 ,若
,若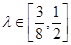 ,求直线AB的斜率的取值范围.
,求直线AB的斜率的取值范围.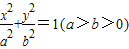 的短轴长与焦距相等,且过定点
的短轴长与焦距相等,且过定点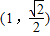 ,倾斜角为
,倾斜角为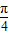 的直线l交椭圆C于A、B两点,线段AB的垂直平分线交x轴于点P.
的直线l交椭圆C于A、B两点,线段AB的垂直平分线交x轴于点P.