题目内容
设等比数列 的前
的前 项和为
项和为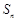 ,若
,若 成等差数列,且
成等差数列,且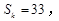
 ,其中
,其中 ,则
,则 的值为 .
的值为 .
135
解析试题分析:设公比为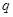 ,由
,由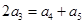 即
即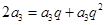 ,解得
,解得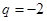 或
或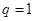 (舍去,因为
(舍去,因为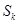 与
与 异号),
异号), ,
,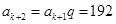 ,
,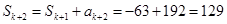 .
.
考点:等比数列的通项和求和.

练习册系列答案
相关题目
题目内容
设等比数列 的前
的前 项和为
项和为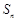 ,若
,若 成等差数列,且
成等差数列,且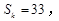
 ,其中
,其中 ,则
,则 的值为 .
的值为 .
135
解析试题分析:设公比为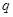 ,由
,由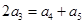 即
即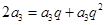 ,解得
,解得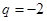 或
或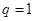 (舍去,因为
(舍去,因为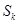 与
与 异号),
异号), ,
,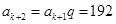 ,
,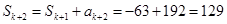 .
.
考点:等比数列的通项和求和.
