题目内容
（2012•许昌县一模）设函数f(x)=sin(2x-
)，x∈R，则f（x）是（ ）
| π |
| 2 |
分析：先利用诱导公式将原函数变换为f（x）=-cos2x，再利用y=Acos（ωx+φ）的周期公式和偶函数的定义证明函数的周期性和奇偶性即可
解答：解：∵函数f(x)=sin(2x-
)=-cos2x
∴f（-x）=-cos（-2x）=-cos2x=f（x）且T=
=π
∴函数f（x）是最小正周期为π的偶函数
故选B
| π |
| 2 |
∴f（-x）=-cos（-2x）=-cos2x=f（x）且T=
| 2π |
| 2 |
∴函数f（x）是最小正周期为π的偶函数
故选B
点评：本题考察了三角函数的图象和性质，y=Acos（ωx+φ）型函数的周期性和奇偶性的判断方法
练习册系列答案
名校课堂系列答案
相关题目
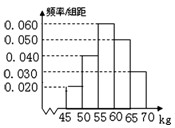（2012•许昌县一模）某学校对高一新生的体重进行了抽样调查．右图是根据抽样调查后的数据绘制的频率分布直方图，其中体重（单位：kg）的范围是[45，70]，样本数据分组为[45，50），[50，55），[55，60），[60，65），[65，70]，已知被调查的学生中体重不足55kg的有36，则被调查的高一新生体重在50kg至65kg的人数是．（ ）
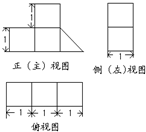（2012•许昌县一模）一个几何体按比例绘制的三视图如图所示（单位：m），则该几何体的体积为（ ）