题目内容
一辆汽车的电路发生故障,电路板上共有10个二极管,只知道其中有两个是不合格,但不知道是哪两个. 现要逐个用仪器进行检测,但受于仪器的限制,最多能检测6个二极管,若将两个不合格的二极管全部查出即停止检测,否则一直检测到6个为止. 设ξ是检查二极管的个数.(1)求ξ的分布列(结果用分数表示);
(2)求检查二极管不超过4个时,已查出两个不合格二极管的概率;
(3)求ξ的数学期望.
【答案】分析:(1)由题意可得:ξ可能取的值为2,3,4,5,6,再结合题意分别求出其发生的概率进而求出ξ的分布列.
(2)由题意知本题是一个等可能事件的概率,结合题意所求事件包括三种情况,即包含以ξ=2,ξ=3,ξ=4,再结合(1)即可得到答案.
(3)由(1)并且结合有关的公式即可得到答案.
解答:解:(1)由题意可得:ξ可能取的值为2,3,4,5,6,
所以P(ξ=2)=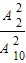 =
= ,P(ξ=3)=
,P(ξ=3)=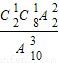 =
=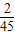 ,P(ξ=4)=
,P(ξ=4)=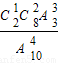 =
=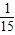 ,P(ξ=5)=
,P(ξ=5)=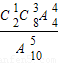 =
=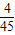 ,P(ξ=6)=
,P(ξ=6)=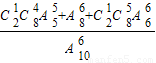 =
= ,
,
所以ξ的分布列为:
(2)由题意知本题是一个等可能事件的概率,
检查二极管不超过4个时,已查出两个不合格二极管包括三种情况,即包含以ξ=2,ξ=3,ξ=4,
并且题意可得这三种情况是互斥的,
∴根据等可能事件的概率和互斥事件的概率公式可得:P=P(ξ=2)+P(ξ=3)+P(ξ=4)=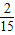 ,
,
∴检查二极管不超过4个时,已查出两个不合格二极管的概率为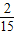 .
.
(3)由(1)可得:Eξ=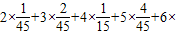
 =
=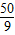 .
.
点评:本题主要考查等可能事件的概率与互斥事件的概率公式,以及考查离散型随机变量的分布列、数学期望与排列组合有关的知识点,解决此题的关键是看清要求概率的事件所包含的结果,再结合题意分类进行求解,在分类时要做到不重不漏.
(2)由题意知本题是一个等可能事件的概率,结合题意所求事件包括三种情况,即包含以ξ=2,ξ=3,ξ=4,再结合(1)即可得到答案.
(3)由(1)并且结合有关的公式即可得到答案.
解答:解:(1)由题意可得:ξ可能取的值为2,3,4,5,6,
所以P(ξ=2)=
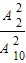 =
= ,P(ξ=3)=
,P(ξ=3)=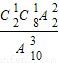 =
=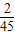 ,P(ξ=4)=
,P(ξ=4)=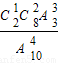 =
=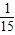 ,P(ξ=5)=
,P(ξ=5)=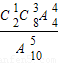 =
=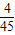 ,P(ξ=6)=
,P(ξ=6)=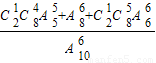 =
= ,
,所以ξ的分布列为:
| ξ | 2 | 3 | 4 | 5 | 6 |
| P | 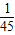 | 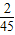 | 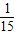 | 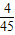 |  |
检查二极管不超过4个时,已查出两个不合格二极管包括三种情况,即包含以ξ=2,ξ=3,ξ=4,
并且题意可得这三种情况是互斥的,
∴根据等可能事件的概率和互斥事件的概率公式可得:P=P(ξ=2)+P(ξ=3)+P(ξ=4)=
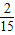 ,
,∴检查二极管不超过4个时,已查出两个不合格二极管的概率为
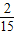 .
.(3)由(1)可得:Eξ=
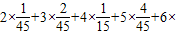
 =
=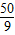 .
.点评:本题主要考查等可能事件的概率与互斥事件的概率公式,以及考查离散型随机变量的分布列、数学期望与排列组合有关的知识点,解决此题的关键是看清要求概率的事件所包含的结果,再结合题意分类进行求解,在分类时要做到不重不漏.

练习册系列答案
相关题目