题目内容
已知集合A={z||z-2|≤2,z∈C},集合B={w|w= zi+b,b∈R},当A∩B=B时,求b的值.
zi+b,b∈R},当A∩B=B时,求b的值.

 zi+b,b∈R},当A∩B=B时,求b的值.
zi+b,b∈R},当A∩B=B时,求b的值. 
2
由w= zi+b得z=
zi+b得z= ,
,
∵z∈A,∴|z-2|≤2,代入得| -2|≤2,化简得|w-(b+i)|≤1
-2|≤2,化简得|w-(b+i)|≤1
∴集合A、B在复平面内对应的点的集合是两个圆面,集合A表示以点(2,0)为圆心,半径为2的圆面,集合B表示以点(b,1)为圆心,半径为1的圆面
又A∩B=B,即B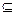 A,∴两圆内含
A,∴两圆内含
因此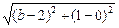 ≤2-1,即(b-2)2≤0,∴b=2.
≤2-1,即(b-2)2≤0,∴b=2.
 zi+b得z=
zi+b得z= ,
,∵z∈A,∴|z-2|≤2,代入得|
 -2|≤2,化简得|w-(b+i)|≤1
-2|≤2,化简得|w-(b+i)|≤1
∴集合A、B在复平面内对应的点的集合是两个圆面,集合A表示以点(2,0)为圆心,半径为2的圆面,集合B表示以点(b,1)为圆心,半径为1的圆面

又A∩B=B,即B
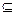 A,∴两圆内含
A,∴两圆内含
因此
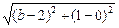 ≤2-1,即(b-2)2≤0,∴b=2.
≤2-1,即(b-2)2≤0,∴b=2.
练习册系列答案
相关题目
 }
}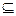 中{a,b},②{(a,b)}={a,b},③{a,b}
中{a,b},②{(a,b)}={a,b},③{a,b} 知集合A={x,
知集合A={x, ,1},B={x2,x+y,0},若A=B,则x2009+y2100=______,
,1},B={x2,x+y,0},若A=B,则x2009+y2100=______, =1,a>0,b>0},当A∩B只有一个元素时,a,b的关系式是_________
=1,a>0,b>0},当A∩B只有一个元素时,a,b的关系式是_________
 ,集合
,集合 则
则 的值是
的值是 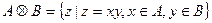 .设
.设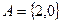 ,
,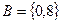 ,则集合
,则集合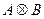 的所有元素之和为( )
的所有元素之和为( ) 的元素个数有( )
的元素个数有( ) ,
, ,且
,且 ,
, 的取值范围是 。
的取值范围是 。