题目内容
对定义域为D的函数,若存在距离为d的两条平行直线l1:y=kx+m1和l2:y=kx+m2,使得当x∈D时,kx+m1≤f(x)≤kx+m2恒成立,则称函数f(x)在x∈D有一个宽度为d的通道.有下列函数:
①f(x)=
;②f(x)=sinx;③f(x)=
;④f(x)=x3+1.
其中在[1,+∞)上通道宽度为1的函数是( )
①f(x)=
| 1 |
| x |
| x2-1 |
其中在[1,+∞)上通道宽度为1的函数是( )
| A、①③ | B、②③ | C、②④ | D、①④ |
练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 如图,D、E分别是AB、AC上两点,CD与BE相交于点O,下列条件中不能使△ABE和△ACD相似的是( )
如图,D、E分别是AB、AC上两点,CD与BE相交于点O,下列条件中不能使△ABE和△ACD相似的是( )| A、∠B=∠C | B、∠ADC=∠AEB | C、BE=CD,AB=AC | D、AD:AC=AE:AB |
在极坐标系中,点F(1,0)到直线θ=
(ρ∈R)的距离是( )
| π |
| 4 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
若关于x的不等式|x-1|+x≤a无解,则实数a的取值范围是( )
| A、(-∞,1) | B、(-∞,1] | C、(1,+∞) | D、[1,+∞) |
已知f(x)是定义在R上的函数,且对任意实数x有f(x+4)=-f(x)+2
,若函数y=f(x-1)的图象关于直线x=1对称,则f(2014)=( )
| 2 |
A、-2+2
| ||
B、2+2
| ||
C、2
| ||
D、
|

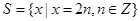 ,
,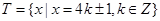 则 ( )
则 ( )

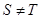

 ,那么集合
,那么集合 等于( )
等于( )