题目内容
8.已知函数f(x)=2cos2x+sin2x+a(a∈R).(1)求函数f(x)的单调增区间;
(2)当x∈[0,$\frac{π}{6}$]时,f(x)的最大值为2+$\sqrt{2}$,求a的值.
分析 (1)利用倍角公式及两角和的正弦变形,然后由复合函数的单调性求得求函数f(x)的单调增区间;
(2)由x的范围求得相位的范围,进一步得到函数的最大值求得a.
解答 解:(1)f(x)=2cos2x+sin2x+a=1+cos2x+sin2x+a
=$\sqrt{2}sin(2x+\frac{π}{4})+a+1$.
由$-\frac{π}{2}+2kπ≤2x+\frac{π}{4}≤\frac{π}{2}+2kπ$,解得:$-\frac{3π}{8}+kπ≤x≤\frac{π}{8}+kπ,k∈Z$.
∴函数f(x)的单调增区间为[$-\frac{3π}{8}+kπ,\frac{π}{8}+kπ$],k∈Z;
(2)当x∈[0,$\frac{π}{6}$]时,$2x+\frac{π}{4}∈[\frac{π}{4},\frac{7π}{12}]$,
∴$f(x)_{max}=\sqrt{2}+a+1=2+\sqrt{2}$,即a=1.
点评 本题考查三角函数值的恒等变换应用,考查了三角函数的图象和性质,是中档题.

练习册系列答案
相关题目
16.已知命题p:x2-x-2>0,q:|x|<a,若¬p是q的必要而不充分条件,则实数a的取值范围是( )
| A. | a<1 | B. | a≤1 | C. | a<2 | D. | a≤2 |
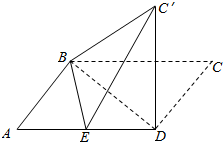 已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点,沿直线BD将△BCD翻折成△BC′D,使得平面BC′D⊥平面ABD.
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点,沿直线BD将△BCD翻折成△BC′D,使得平面BC′D⊥平面ABD.