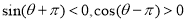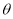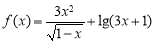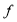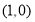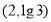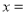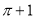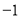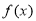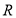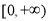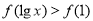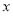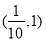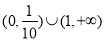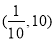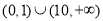题目内容
已知函数 .
.
(1)求函数定义域和函数图像所过的定点;
(2)若已知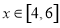 时,函数最大值为2,求
时,函数最大值为2,求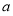 的值.
的值.
(1)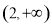 ,
, ;(2)
;(2)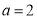
【解析】
试题分析:(1)根据对数的真数大于0,可求得定义域,再根据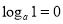 可求得所过定点。(2)根据
可求得所过定点。(2)根据 的范围先求整体真数的范围,再根据对数的单调性求值域,得到最大值是其等于2,解出a。但这道题给的是
的范围先求整体真数的范围,再根据对数的单调性求值域,得到最大值是其等于2,解出a。但这道题给的是 ,所以需分两种情况讨论。
,所以需分两种情况讨论。
试题解析:(1)令 ,解得
,解得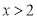 ,故定义域为
,故定义域为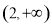
令 ,解得
,解得 ,故函数过定点
,故函数过定点
(2)若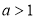 ,函数
,函数 在
在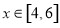 上单调递增,
上单调递增,
故 时
时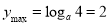 ,解得
,解得 ;
;
若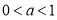 ,函数
,函数 在
在 上单调递减,
上单调递减,
故 时
时 ,解得
,解得 ;
;
综上,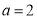 。
。
考点:对数函数的定义域,定点和单调性

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目