题目内容
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,AC⊥BC,AC=BC= ![]() AA1=2,D是AC的中点.
AA1=2,D是AC的中点. 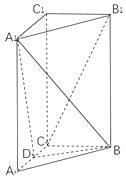
(1)求证:B1C∥平面A1BD;
(2)求直线AC与平面A1BD所成角的正弦值.
【答案】
(1)证明:连接AB1交A1B于O,则O为AB1的中点,连接OD,
又D是AC的中点,∴OD∥B1C,
又OD平面A1BD,B1C平面A1BD,
∴B1C∥平面A1BD;
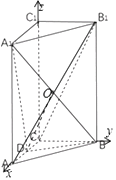
(2)解:∵AA1⊥底面ABC,AC⊥BC,
∴分别以CA、CB、CC1所在直线为x、y、z轴建立空间直角坐标系,
∵AC=BC= ![]() AA1=2,
AA1=2,
∴C(0,0,0),A(2,0,0),D(1,0,0),B(0,2,0),
A1(2,0,4),
则 ![]() ,
, ![]() ,
, ![]() ,
,
设平面A1BD的一个法向量为 ![]() ,
,
由 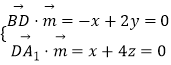 ,取z=﹣1,得
,取z=﹣1,得 ![]() ,
,
∴直线AC与平面A1BD所成角的正弦值为sinθ=| ![]() |=|
|=| ![]() |=
|= ![]() .
.
【解析】(1)连接AB1交A1B于O,则O为AB1的中点,连接OD,结合D是AC的中点,可得OD∥B1C,再由线面平行的判定得B1C∥平面A1BD;(2)由AA1⊥底面ABC,AC⊥BC,分别以CA、CB、CC1所在直线为x、y、z轴建立空间直角坐标系,求出所用点的坐标,进一步求出 ![]() 及平面A1BD的一个法向量的坐标,由两向量所成角的余弦值可得直线AC与平面A1BD所成角的正弦值.
及平面A1BD的一个法向量的坐标,由两向量所成角的余弦值可得直线AC与平面A1BD所成角的正弦值.
【考点精析】利用直线与平面平行的判定和空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则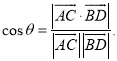 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目