题目内容
已知在Rt△ABC中,∠ACB=90°,BC=4,AC=3,点P是AB上一动点.建立适当的坐标系,求直线AB的方程.
【答案】分析:以C为坐标原点,CB所在的直线为x轴,CA所在的直线为y轴,建立平面直角坐标系,找到A和B的坐标后就能求出直线AB的方程.
解答:解:以C为坐标原点,CB所在的直线为x轴,CA所在的直线为y轴,建立平面直角坐标系,
则A(0,3),B(4,0),
直线AB的方程为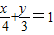 .
.
整理,得3x+4y-12=0.
点评:恰当地建立平面直角坐标系,能够有效地简化轨迹方程.
解答:解:以C为坐标原点,CB所在的直线为x轴,CA所在的直线为y轴,建立平面直角坐标系,
则A(0,3),B(4,0),
直线AB的方程为
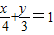 .
.整理,得3x+4y-12=0.
点评:恰当地建立平面直角坐标系,能够有效地简化轨迹方程.

练习册系列答案
相关题目