题目内容
已知在Rt△ABC中,若∠C=90°,则cos2A+cos2B=1;在立体几何中,给出四面体性质的猜想.
思路分析:考虑到平面中的图形是直角三角形,所以我们在空间选取有3个面两两垂直的直四面体P—A′B′C′,且三个面分别与面A′B′C′所成的二面角为α、β、γ.
解:如图2-1-2所示,在Rt△ABC中,cos2A+cos2B=(![]() )2+
)2+![]() =1.
=1.
于是把结论类比到四面体P—A′B′C′中,我们猜想,三棱锥P-A′B′C′中,若三个侧面PA′B′,PB′C′,PC′A′两两互相垂直,且分别与底面所成的角为α、β、γ,则cos2α+cos2β+cos2γ=1.
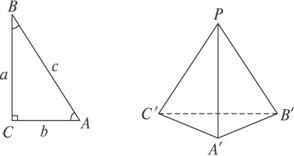
图2-1-2
深化升华 类比推理应从具体问题出发,通过观察、分析、联想进行对比,归纳,提出猜想.

练习册系列答案
相关题目