题目内容
在等比数列中,a1=
,q=
,an=
,则项数n为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 32 |
5
5
.分析:已知等比数列的首项和公比可以求出等比数列的通项公式,再根据通项公式进行求解;
解答:解:在等比数列中,a1=
,q=
,
∴an=
×(
)n-1=(
)n,
∵an=
,
∴(
)n=
,
解得n=5,
故答案为5;
| 1 |
| 2 |
| 1 |
| 2 |
∴an=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵an=
| 1 |
| 32 |
∴(
| 1 |
| 2 |
| 1 |
| 32 |
解得n=5,
故答案为5;
点评:此题主要考查等比数列的性质及其通项公式的应用,是一道基础题;

练习册系列答案
相关题目
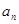 }中,a1=1,公比|q|≠1,若
}中,a1=1,公比|q|≠1,若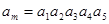 ,则m=_________
,则m=_________