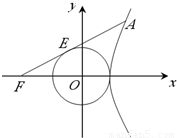
题目内容
 左焦点为F的双曲线C:
左焦点为F的双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
(
,+∞)
| 2 |
(
,+∞)
.| 2 |
分析:利用直线FA与圆x2+y2=a2相切,可求得切线的斜率为
,再分析出切线AF的斜率小于渐进线y=
x的斜率
,即可求得双曲线C的离心率取值范围.
| a |
| b |
| b |
| a |
| b |
| a |
解答:解:设直线FA的方程为:y=k(x+c),∵直线FA与x2+y2=a2相切,
∴a=
,
∴a2+a2k2=c2k2,
∴b2k2=a2,又k>0,
∴k=
,
∵切线与右支有交点A,则切线AF的斜率小于渐进线y=
x的斜率
,
即
<
,
∴a2<b2,又b2=c2-a2,
∴c2>2a2.
∴e2=
>2,
∴e>
.
∴a=
| |ck| | ||
|
∴a2+a2k2=c2k2,
∴b2k2=a2,又k>0,
∴k=
| a |
| b |
∵切线与右支有交点A,则切线AF的斜率小于渐进线y=
| b |
| a |
| b |
| a |
即
| a |
| b |
| b |
| a |
∴a2<b2,又b2=c2-a2,
∴c2>2a2.
∴e2=
| c2 |
| a2 |
∴e>
| 2 |
点评:本题考查双曲线的简单性质,分析出切线AF的斜率小于渐进线y=
x的斜率
是关键,考查分析与运算能力,属于中档题.
| b |
| a |
| b |
| a |

练习册系列答案
相关题目
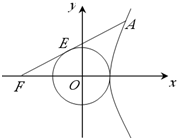 左焦点为F的双曲线
左焦点为F的双曲线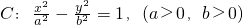 的右支上存在点A,使得直线FA与圆x2+y2=a2相切,则双曲线C的离心率取值范围是________.
的右支上存在点A,使得直线FA与圆x2+y2=a2相切,则双曲线C的离心率取值范围是________.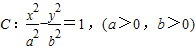 的右支上存在点A,使得直线FA与圆x2+y2=a2相切,则双曲线C的离心率取值范围是 .
的右支上存在点A,使得直线FA与圆x2+y2=a2相切,则双曲线C的离心率取值范围是 .