题目内容
在平面直角坐标系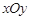 中,以坐标原点
中,以坐标原点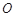 为极点,
为极点,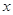 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线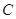 的极坐标方程为
的极坐标方程为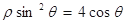 ,直线
,直线 的参数方程为
的参数方程为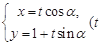 为参数,
为参数,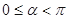 ).
).
(1)化曲线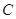 的极坐标方程为直角坐标方程;
的极坐标方程为直角坐标方程;
(2)若直线 经过点
经过点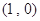 ,求直线
,求直线 被曲线
被曲线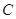 截得的线段
截得的线段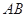 的长.
的长.
(1) 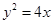 ;(2)8
;(2)8
解析试题分析:(1)极坐标化为直角坐标的基本公式是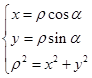 ,本小题要在极坐标方程的两边乘以一个
,本小题要在极坐标方程的两边乘以一个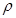 .再根据基本转化公式,即可化简.
.再根据基本转化公式,即可化简.
(2)解(一)将直线的参数方程化为直角方程,在联立抛物线方程,消去y即可得到一个关于x的一元二次方程,从而利用韦达定理,以及弦长公式求出弦长.解(二)由直线的参数方程与抛物线方程联立.再根据弦长公式,利用韦达定理即可求出弦长.
试题解析:解法(一):(1)由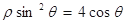 得
得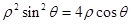 ,即曲线C的直角坐标方程为
,即曲线C的直角坐标方程为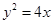 .
.
(2)由直线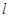 经过点(1,0),得直线
经过点(1,0),得直线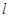 的直角坐标系方程是
的直角坐标系方程是 ,联立
,联立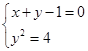 ,消去y,得
,消去y,得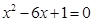 ,又点(1,0)是抛物线的焦点,由抛物线定义,得弦长
,又点(1,0)是抛物线的焦点,由抛物线定义,得弦长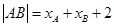 =6+2=8.
=6+2=8.
解法(二):(1)同解法一.
(2)由直线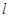 经过点(1,0),得
经过点(1,0),得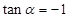 ,直线
,直线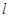 的参数方程为
的参数方程为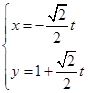 将直线
将直线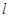 的参数方程代入
的参数方程代入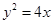 ,得
,得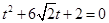 ,所以
,所以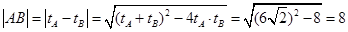 .
.
考点:1.极坐标方程.2.参数方程.3.直线与抛物线的弦长公式.

练习册系列答案
相关题目
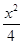 +y2=1上的三个点,O是坐标原点.
+y2=1上的三个点,O是坐标原点.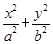 =1(a>b>0)的右焦点为F2(1,0),点A
=1(a>b>0)的右焦点为F2(1,0),点A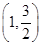 在椭圆上.
在椭圆上.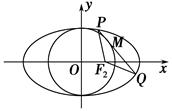
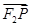 |+|
|+|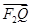 |+|
|+|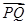 |是否为定值?如果是,求出该定值;如果不是,说明理由.
|是否为定值?如果是,求出该定值;如果不是,说明理由. 的焦点为双曲线
的焦点为双曲线 的一个焦点,且两条曲线都经过点
的一个焦点,且两条曲线都经过点 .
. 在抛物线上,且它与双曲线的左,右焦点构成的三角形的面积为4,求点
在抛物线上,且它与双曲线的左,右焦点构成的三角形的面积为4,求点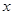 轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.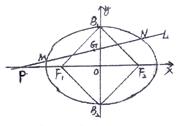
 =1(a>b>0)的两个焦点F1,F2和上下两个顶点B1,B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点.
=1(a>b>0)的两个焦点F1,F2和上下两个顶点B1,B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点.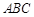 的两个顶点
的两个顶点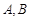 的坐标分别是
的坐标分别是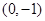 ,
,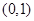 ,且
,且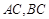 所在直线的斜率之积等于
所在直线的斜率之积等于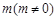 .
.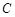 的轨迹
的轨迹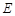 的方程,并判断轨迹
的方程,并判断轨迹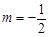 时,过点
时,过点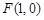 的直线
的直线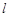 交曲线
交曲线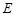 于
于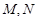 两点,设点
两点,设点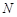 关于
关于 轴的对称点为
轴的对称点为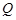 (
(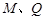 不重合), 试问:直线
不重合), 试问:直线 与
与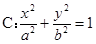
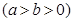 过点
过点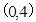 ,离心率为
,离心率为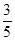 .
.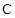 的方程;
的方程;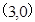 且斜率为
且斜率为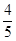 的直线被椭圆所截得线段的中点坐标.
的直线被椭圆所截得线段的中点坐标.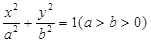 上的点
上的点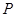 到左右两焦点
到左右两焦点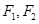 的距离之和为
的距离之和为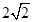 ,离心率为
,离心率为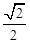 .
.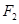 的直线
的直线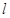 交椭圆于
交椭圆于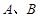 两点,若
两点,若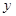 轴上一点
轴上一点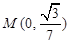 满足
满足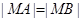 ,求直线
,求直线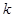 的值.
的值.