题目内容
在△ABC中AB=2,C=30°,则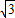 BC-AC 的最大值是( )
BC-AC 的最大值是( )A.4
B.
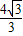
C.
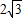
D.
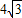
【答案】分析:有正弦定理以及A+B=150°可得 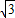 BC-AC=
BC-AC=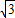 •4sinA-4sinB=4sin(A-30°),再根据-30°<A-30°<120°,可得4sin(A-30°)的最大值.
•4sinA-4sinB=4sin(A-30°),再根据-30°<A-30°<120°,可得4sin(A-30°)的最大值.
解答:解:∵在△ABC中AB=2,C=30°,则有正弦定理可得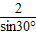 =
=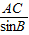 =
= =4,
=4,
又A+B=150°,∴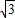 BC-AC=
BC-AC= •4sinA-4sinB=8(
•4sinA-4sinB=8(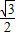 sinA-
sinA- sinB)=8[
sinB)=8[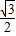 sinA-
sinA- sin(150°-A)]=4[
sin(150°-A)]=4[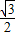 sinA-
sinA- cosA]=4sin(A-30°).
cosA]=4sin(A-30°).
由于-30°<A-30°<120°,故 sin(A-30°)的最大值为1,故4sin(A-30°)的最大值为4,
故选A.
点评:本题主要考查正弦定理以及三角函数恒等变换,正弦函数的定义域和值域,属于中档题.
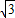 BC-AC=
BC-AC=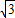 •4sinA-4sinB=4sin(A-30°),再根据-30°<A-30°<120°,可得4sin(A-30°)的最大值.
•4sinA-4sinB=4sin(A-30°),再根据-30°<A-30°<120°,可得4sin(A-30°)的最大值.解答:解:∵在△ABC中AB=2,C=30°,则有正弦定理可得
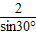 =
=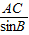 =
= =4,
=4,又A+B=150°,∴
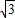 BC-AC=
BC-AC= •4sinA-4sinB=8(
•4sinA-4sinB=8(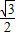 sinA-
sinA- sinB)=8[
sinB)=8[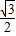 sinA-
sinA- sin(150°-A)]=4[
sin(150°-A)]=4[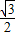 sinA-
sinA- cosA]=4sin(A-30°).
cosA]=4sin(A-30°).由于-30°<A-30°<120°,故 sin(A-30°)的最大值为1,故4sin(A-30°)的最大值为4,
故选A.
点评:本题主要考查正弦定理以及三角函数恒等变换,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 BC-AC 的最大值是
BC-AC 的最大值是

