Question

（2013•怀化三模）已知m＞0，f（x）是定义在R上周期为4的函数，在x∈（-1，3]上f（x）=

m(1-|k|)，k∈(-1，1] -cos πx 2 ，k∈(1，3]

，若方程f（x）=

x

3

恰有5个实数解，则m的取值范围是（　　）

• A．（

  4

  3

  ，

  8

  3

  ）
• B．[

  4

  3

  ，

  8

  3

  ]
• C．[

  4

  3

  ，+∞]
• D．（

  4

  3

  ，+∞）

Answer 1

分析：将方程f（x）=

x

3

恰有5个实数解，转化为一个函数y=f（x）的图象与直线y=

x

3

的位置关系研究即可得出答案．

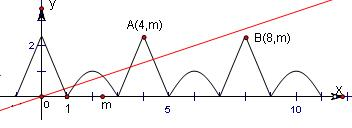解答：解：方程f（x）=

x

3

，
令 y=f（x）=

m(1-|x|)，x∈(-1，1] -cos πx 2 ，x∈(1，3]

，y=

x

3

，
分别画出它们的图象，如图，其中A（4，m），B（8，m）．由图可知，
若方程f（x）=

x

3

恰有5个实数解，
则点A必须在直线y=

x

3

的上方，点B在直线y=

x

3

的下方，即

m＞ 1 3 ×4 m＜ 1 3 ×8

，
∴m∈（

4

3

，

8

3

）
则m的取值范围是（

4

3

，

8

3

）．
故选A．

点评：本题主要考查根的存在性及根的个数判断，解答关键是利用直线与曲线的位置关系，要注意数形结合及转化思想的应用．