题目内容
已知椭圆 +
+ =1(a>1)的左右焦点为F1,F2,抛物线C:y2=2px以F2为焦点且与椭圆相交于点M(x1,y1)、N(x2,y2),点M在x轴上方,直线F1M与抛物线C相切.
=1(a>1)的左右焦点为F1,F2,抛物线C:y2=2px以F2为焦点且与椭圆相交于点M(x1,y1)、N(x2,y2),点M在x轴上方,直线F1M与抛物线C相切.(1)求抛物线C的方程和点M、N的坐标;
(2)设A,B是抛物线C上两动点,如果直线MA,MB与y轴分别交于点P,Q.△MPQ是以MP,MQ为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.
【答案】分析:(1)由c2=a2-b2即可得到椭圆的焦点,进而得到p即抛物线的方程,设点M的坐标写出方程,与抛物线的方程联立,消去一个未知数得到关于另一个未知数的一元二次方程,由相切得到判别式△=0即可求出;
(2)设A ,B
,B .即可表示出kMA,kMB,由△MPQ是以MP,MQ为腰的等腰三角形,可得kMA=-kMB.进而可证明kAB为定值.
.即可表示出kMA,kMB,由△MPQ是以MP,MQ为腰的等腰三角形,可得kMA=-kMB.进而可证明kAB为定值.
解答:解:(1)由椭圆方程得半焦距 =1.
=1.
∴椭圆焦点为F1(-1,0),F2(1,0).
又抛物线C的焦点为 ,∴
,∴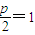 ,解得p=2.∴抛物线C的方程:y2=4x.
,解得p=2.∴抛物线C的方程:y2=4x.
∵点M(x1,y1)在抛物线C上,
∴ ,直线F1M的方程为
,直线F1M的方程为 .
.
代入抛物线C得 ,即
,即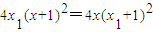 .
.
∴
∵F1M与抛物线C相切,∴△= =0,∴x1=1.
=0,∴x1=1.
∴M、N的坐标分别为(1,2)、(1,-2).
(2)直线AB的斜率为定值-1.
证明如下:设A ,B
,B .
.
则 =
=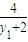 ,同理
,同理 ,
,
∵△MPQ是以MP,MQ为腰的等腰三角形,∴kMA=-kMB.
即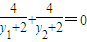 ,
,
化为y1+y2+4=0得y1+y2=-4.
∴kAB= =
= =
= =-1.
=-1.
所以直线AB的斜率为定值-1.
点评:熟练掌握椭圆、抛物线的标准方程及其性质、直线与曲线相交相切问题转化为方程联立得到一元二次方程得根与系数的关系及△≥0、△MPQ是以MP、MQ为腰的等腰三角形可得kMA=-kMB等设解题的关键.
(2)设A
 ,B
,B .即可表示出kMA,kMB,由△MPQ是以MP,MQ为腰的等腰三角形,可得kMA=-kMB.进而可证明kAB为定值.
.即可表示出kMA,kMB,由△MPQ是以MP,MQ为腰的等腰三角形,可得kMA=-kMB.进而可证明kAB为定值.解答:解:(1)由椭圆方程得半焦距
 =1.
=1.∴椭圆焦点为F1(-1,0),F2(1,0).
又抛物线C的焦点为
 ,∴
,∴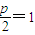 ,解得p=2.∴抛物线C的方程:y2=4x.
,解得p=2.∴抛物线C的方程:y2=4x.∵点M(x1,y1)在抛物线C上,
∴
 ,直线F1M的方程为
,直线F1M的方程为 .
.代入抛物线C得
 ,即
,即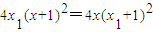 .
.∴

∵F1M与抛物线C相切,∴△=
 =0,∴x1=1.
=0,∴x1=1.∴M、N的坐标分别为(1,2)、(1,-2).
(2)直线AB的斜率为定值-1.
证明如下:设A
 ,B
,B .
.则
 =
=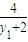 ,同理
,同理 ,
,∵△MPQ是以MP,MQ为腰的等腰三角形,∴kMA=-kMB.
即
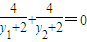 ,
,化为y1+y2+4=0得y1+y2=-4.
∴kAB=
 =
= =
= =-1.
=-1.所以直线AB的斜率为定值-1.
点评:熟练掌握椭圆、抛物线的标准方程及其性质、直线与曲线相交相切问题转化为方程联立得到一元二次方程得根与系数的关系及△≥0、△MPQ是以MP、MQ为腰的等腰三角形可得kMA=-kMB等设解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 ,则椭圆方程为( )
,则椭圆方程为( ) +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 . +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则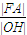 的最大值为 .
的最大值为 . +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 . =1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若
=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若 (应为PB),则离心率为
(应为PB),则离心率为 B、
B、 C、
C、 D、
D、