题目内容
已知椭圆 +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则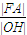 的最大值为 .
的最大值为 .
【答案】分析:椭圆属于解析几何的版块,常用解析法处理.所以我们要数形互化,把问题中的几何最值转化为代数最值,运用解析法,即“算”的办法解决.通过观察不难发现,|FA|与|OH|都可以用椭圆中一些基本的参量表示出来,例如,|FA|即为该椭圆右定点与右焦点间的距离,即|FA|=|OA|-|OF|,而|OA|即为椭圆的长半轴长a,|OF|即为椭圆的半焦距长c,∴|FA|=a-c.当完成这些工作后,我们只要对得到的表达式在其可行域内求最值即可.
解答:解:依题意得,|FA|即为该椭圆右定点与右焦点间的距离,即|FA|=|OA|-|OF|,
又∵|OA|即为椭圆的长半轴长a,|OF|即为椭圆的半焦距长c,
∴|FA|=a-c.
又∵H为椭圆的右准线与x轴的交点,故|OH|即为椭圆中心到右准线的距离,依准线的定义知,|OH|=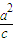 ,则
,则 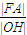 =
=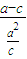 ①
①
又∵椭圆的离心率e=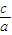 ,(0<e<1),从而c=ae,代入①,得
,(0<e<1),从而c=ae,代入①,得 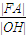 =
=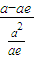 =e(1-e)=-
=e(1-e)=- +
+ (0<e<1),
(0<e<1),
当且仅当e= 时
时  取得最值
取得最值  .
.
故答案为: .
.
点评:最值问题是高考的热点之一.常用的方法有构建函数模型法,基本不等式法等.对于一元表达式,我们采用第一种方法,对于二元的则采用后者.本体看似是二元表达式,但通过e的代换后发现,其实际是一元二次函数,这就转化为我们熟悉的函数模型,一切问题也变得简单起来.
解答:解:依题意得,|FA|即为该椭圆右定点与右焦点间的距离,即|FA|=|OA|-|OF|,
又∵|OA|即为椭圆的长半轴长a,|OF|即为椭圆的半焦距长c,
∴|FA|=a-c.
又∵H为椭圆的右准线与x轴的交点,故|OH|即为椭圆中心到右准线的距离,依准线的定义知,|OH|=
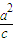 ,则
,则 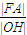 =
=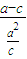 ①
①又∵椭圆的离心率e=
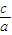 ,(0<e<1),从而c=ae,代入①,得
,(0<e<1),从而c=ae,代入①,得 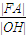 =
=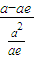 =e(1-e)=-
=e(1-e)=- +
+ (0<e<1),
(0<e<1),当且仅当e=
 时
时  取得最值
取得最值  .
.故答案为:
 .
.点评:最值问题是高考的热点之一.常用的方法有构建函数模型法,基本不等式法等.对于一元表达式,我们采用第一种方法,对于二元的则采用后者.本体看似是二元表达式,但通过e的代换后发现,其实际是一元二次函数,这就转化为我们熟悉的函数模型,一切问题也变得简单起来.

练习册系列答案
相关题目
 ,则椭圆方程为( )
,则椭圆方程为( ) +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 . +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 . =1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若
=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若 (应为PB),则离心率为
(应为PB),则离心率为 B、
B、 C、
C、 D、
D、