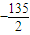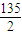题目内容
若在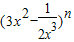 的展开式中含有常数项,则正整数n取得最小值时常数项为( )
的展开式中含有常数项,则正整数n取得最小值时常数项为( )A.
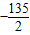
B.-135
C.
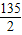
D.135
【答案】分析:通过二项展开式的通项公式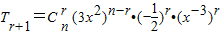 ,令x的次数为0即可求得正整数n取得最小值时常数项.
,令x的次数为0即可求得正整数n取得最小值时常数项.
解答:解:∵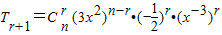 =
=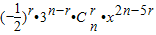 ,
,
∴2n-5r=0,又n∈N*,r≥0,
∴n=5,r=2时满足题意,此时常数项为: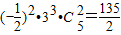 ;
;
故选C.
点评:本题考查二项式定理的应用,关键在于应用二项展开式的通项公式,注重分析与计算能力的考查,属于中档题.
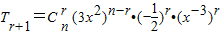 ,令x的次数为0即可求得正整数n取得最小值时常数项.
,令x的次数为0即可求得正整数n取得最小值时常数项.解答:解:∵
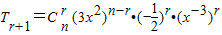 =
=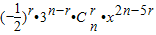 ,
,∴2n-5r=0,又n∈N*,r≥0,
∴n=5,r=2时满足题意,此时常数项为:
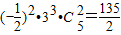 ;
;故选C.
点评:本题考查二项式定理的应用,关键在于应用二项展开式的通项公式,注重分析与计算能力的考查,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
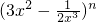 的展开式中含有常数项,则正整数n取得最小值时常数项为
的展开式中含有常数项,则正整数n取得最小值时常数项为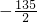
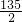
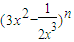 的展开式中含有常数项,则正整数n取得最小值时常数项为( )
的展开式中含有常数项,则正整数n取得最小值时常数项为( )