Question

已知函数f(x)=2^x+a的反函数是y=f ^-1 (x).设P(x+a,y₁)、Q(x,y₂)、R(2+a,y₃)是y= f ^-1 (x)图象上不同的三点.

(1)如果存在正实数x,使y₁、y₂、y₃成等差数列，试用x表示a;?

(2)在(1)的条件下，如果实数x是唯一的，试求a的取值范围.?

Answer 1

解析:（1）易知函数f(x)的反函数?

f ^-1(x)=log₂(x-a)(x＞a).?

∵P、Q、R是f ^-1 (x)图象上不同的三点,??

∴y₁=log₂x,y₂=log₂(x-a),y₃=1.?

又∵P、Q、R为不同的三点，?

∴a≠0且x≠2.?

又已知y₁,y₂,y₃成等差数列，即有y₁+y₃=2y₂,??

因此，1+log₂x=2log₂(x-a),?

即log₂2x=log₂(x-a).?

故x-a=2x，x＞0且x＞a.?

∴a=x-2x(x＞0且x≠2).①?

（2）等量关系①等价于?

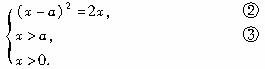
方程②等价于x²-2(a+1)x+a²=0.?④?

Δ=［2(a+1)］²-4a²=8a+4.?

当a=-时，Δ=0.?

方程④仅有一个实数解x=且满足③,??

∴a=-满足①有唯一解.?

当a＞-时，Δ＞0,方程②有两个相异实数解，即?

x₁=a+1+,x₂=a+1-,?

又x₁=a+1+＞a,?

∴x₁＞a满足条件③.?

∴x₁是方程①的解.?

要使方程①有唯一解，则x₂不能是①的解，?

∴x₂=a+1-≤a, ≥1,即a≥0.?

∵a≠0,∴a＞0.?

综合和，a的取值范围是a=-或a＞0.