题目内容
【题目】点A、B分别是椭圆![]() 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于![]() 轴上方,
轴上方,![]() .
.
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于![]() ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离![]() 的最小值.
的最小值.
【答案】(1)(![]() ,
,![]() ).(2)
).(2)![]()
【解析】
(1)根据条件列关于P点坐标得方程组,解得结果,(2)先根据点到直线距离公式结合条件解得点M坐标,再建立![]() 的函数解析式,最后根据二次函数性质求最小值.
的函数解析式,最后根据二次函数性质求最小值.
解:(1)由已知可得点A(-6,0),F(4,0)
设点P(![]() ,
,![]() ),则
),则![]() ={
={![]() +6,
+6,![]() },
},![]() ={
={![]() -4,
-4,![]() },
},
由已知可得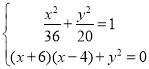
则2![]() +9
+9![]() -18=0,解得
-18=0,解得![]() =
=![]() 或
或![]() =-6.
=-6.
由于![]() >0,只能
>0,只能![]() =
=![]() ,于是
,于是![]() =
=![]() .
.
∴点P的坐标是(![]() ,
,![]() ).
).
(2)直线AP的方程是![]() -
-![]()
![]() +6=0.
+6=0.
设点M(![]() ,0),则M到直线AP的距离是
,0),则M到直线AP的距离是![]() .
.
于是![]() =
=![]() ,又-6≤
,又-6≤![]() ≤6,解得
≤6,解得![]() =2.
=2.
椭圆上的点(![]() ,
,![]() )到点M的距离为
)到点M的距离为![]() ,
,
则![]() ,
,
由于-6≤![]() ≤6, ∴当
≤6, ∴当![]() =
=![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.

 新思维寒假作业系列答案
新思维寒假作业系列答案【题目】为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 | 发病 | 合计 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合计 | 100 | 100 | 200 |
(附: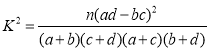 )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
则下列说法正确的:( )
A.至少有99.9%的把握认为“发病与没接种疫苗有关”
B.至多有99%的把握认为“发病与没接种疫苗有关”
C.至多有99.9%的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有0.01%
【题目】新高考方案的实施,学生对物理学科的选择成了焦点话题. 某学校为了了解该校学生的物理成绩,从![]() ,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到
,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到![]() 班学生物理成绩的频率分布直方图和
班学生物理成绩的频率分布直方图和![]() 班学生物理成绩的频数分布条形图.
班学生物理成绩的频数分布条形图.

(Ⅰ)估计![]() 班学生物理成绩的众数、中位数(精确到
班学生物理成绩的众数、中位数(精确到![]() )、平均数(各组区间内的数据以该组区间的中点值为代表);
)、平均数(各组区间内的数据以该组区间的中点值为代表);
(Ⅱ)填写列联表,并判断是否有![]() 的把握认为物理成绩与班级有关?
的把握认为物理成绩与班级有关?
物理成绩 | 物理成绩 | 合计 | |
| |||
| |||
合计 |
附:![]() 列联表随机变量
列联表随机变量![]() ;
;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某中学举行“新冠肺炎”防控知识闭卷考试比赛,总分获得一等奖、二等奖、三等奖的代表队人数情况如表,其中一等奖代表队比三等奖代表队多10人.该校政教处为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插抽奖活动.并用分层抽样的方法从三个代表队中共抽取16人在前排就坐,其中二等奖代表队有5人(同队内男女生仍采用分层抽样)
名次 性别 | 一等奖 代表队 | 二等奖 代表队 | 三等奖 代表队 |
男生 | ? | 30 | ◎ |
女生 | 30 | 20 | 30 |
(1)从前排就坐的一等奖代表队中随机抽取3人上台领奖,用X表示女生上台领奖的人数,求X的分布列和数学期望E(X).
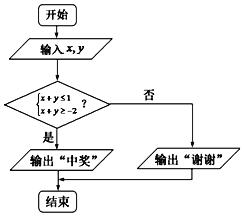
(2)抽奖活动中,代表队员通过操作按键,使电脑自动产生[﹣2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序.若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖.求代表队队员获得奖品的概率.