题目内容
【题目】已知函数f(x)=(sinx+cosx)2+2cos2x﹣2.
(1)求函数f(x)的最小正周期和单调增区间;
(2)当x∈[ ![]() ,
, ![]() ]时,求函数f(x)的最大值,最小值.
]时,求函数f(x)的最大值,最小值.
【答案】
(1)解:f(x)=(sinx+cosx)2+2cos2x﹣2=1+sin2x+cos2x﹣1= ![]() sin(2x+
sin(2x+ ![]() ),
),
∴f(x)的最小正周期是 ![]() =π.
=π.
令﹣ ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,解得﹣
+2kπ,解得﹣ ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,
+kπ,
∴f(x)的单调增区间是[﹣ ![]() +kπ,
+kπ, ![]() +kπ],k∈Z.
+kπ],k∈Z.
(2)解:∵x∈[ ![]() ,
, ![]() ],∴2x+
],∴2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
∴当2x+ ![]() =
= ![]() 时,f(x)取得最大值1,
时,f(x)取得最大值1,
当2x+ ![]() =
= ![]() 时,f(x)取得最小值﹣
时,f(x)取得最小值﹣ ![]() .
.
【解析】(1)化简得f(x)=1+sin2x+cos2x﹣1= ![]() sin(2x+
sin(2x+ ![]() ),令﹣
),令﹣ ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ解得增区间;(2)根据x的范围求出2x+
+2kπ解得增区间;(2)根据x的范围求出2x+ ![]() 的范围,结合正弦函数的单调性求出f(x)的最值.
的范围,结合正弦函数的单调性求出f(x)的最值.
【考点精析】本题主要考查了三角函数的最值的相关知识点,需要掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.

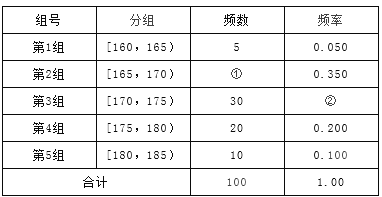
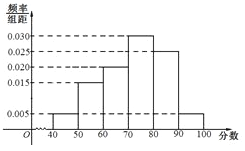
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
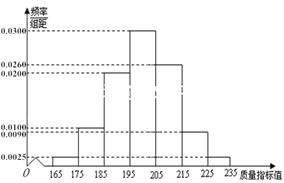
(Ⅰ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定?
(Ⅱ)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(Ⅲ)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
【题目】汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
(1)求![]() 的值;
的值;
(2)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取
2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:
类舒适型轿车中抽取8辆,经检测它们的得分如下:![]() . 把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对 值不超过
. 把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对 值不超过![]() 的概率.
的概率.
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
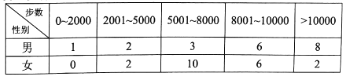
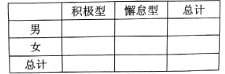
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附: 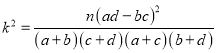 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.