题目内容
直线y=kx+1与双曲线3x2-y2=1相交于A.B两点,O为坐标原点.
(1)若k=1(2),求△AOB的面积
(3)若A.B在双曲线的左右两支上,求k的取值范围.
(1)若k=1(2),求△AOB的面积
(3)若A.B在双曲线的左右两支上,求k的取值范围.
分析:(1)根据弦长公式求出|AB|,利用点到直线的距离公式求出点O到直线AB的距离,利用三角形面积公式即可求得△AOB的面积;
(2)设A(x1,y1),B(x2,y2),因为A,B在双曲线的左右两支上,所以有x1x2<0,根据韦达定理即可得不等式,解出即可;
(2)设A(x1,y1),B(x2,y2),因为A,B在双曲线的左右两支上,所以有x1x2<0,根据韦达定理即可得不等式,解出即可;
解答:解:(1)当k=1时,y=x+1,
由
得,x2-x-1=0,
设A(x1,y1),B(x2,y2),则x1+x2=1,x1x2=-1,
所以|AB|=
|x1-x2|=
•
=
•
=
,
点O到直线AB的距离为d=
,
所以△AOB的面积为:
×|AB|•d=
×
×
=
;
(2)由
,得(3-k2)x2-2kx-2=0,
因为A.B在双曲线的左右两支上,所以
,解得-
<k<
,
所以实数k的取值范围为:-
<k<
.
由
|
设A(x1,y1),B(x2,y2),则x1+x2=1,x1x2=-1,
所以|AB|=
| 2 |
| 2 |
| (x1+x2)2-4x1x2 |
| 2 |
| 12-4(-1) |
| 10 |
点O到直线AB的距离为d=
| 1 | ||
|
所以△AOB的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 1 | ||
|
| ||
| 2 |
(2)由
|
因为A.B在双曲线的左右两支上,所以
|
| 3 |
| 3 |
所以实数k的取值范围为:-
| 3 |
| 3 |
点评:本题考查直线与圆锥曲线的位置关系、弦长公式、点到直线的距离公式及三角形的面积公式,考查学生对基本公式的熟练运用,属中档题.

练习册系列答案
相关题目
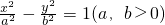 的虚轴长为2
的虚轴长为2 ,渐近线方程是y=
,渐近线方程是y=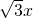 ,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且
,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且 .
. 的虚轴长为2
的虚轴长为2 ,渐近线方程是y=
,渐近线方程是y= ,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且
,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且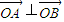 .
.