题目内容
(本题满分分)本题共有小题,第小题满分分,第小题满分分,第小已知函数![]() ,
,![]() 、
、![]() 是
是![]() 图像上两点.
图像上两点.
(1)若![]() ,求证:
,求证:![]() 为定值;
为定值;
(2)设![]() ,其中
,其中![]() 且
且![]() ,求
,求![]() 关于
关于![]() 的解析式;
的解析式;
(3)对(2)中的![]() ,设数列
,设数列![]() 满足
满足![]() ,当
,当![]() 时,
时,![]() ,问是否存在角
,问是否存在角![]() ,使不等式
,使不等式 …
… 对一切
对一切![]() 都成立?若存在,求出角
都成立?若存在,求出角![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(1)![]() 为定值
为定值![]() (2)
(2) ![]() (3)存在
(3)存在![]()
解析:
(1)当![]() 时,
时,
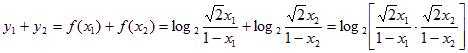
![]() ,所以
,所以![]() 为定值
为定值![]() .…………(4分)
.…………(4分)
(2)由(1)得,![]() (
(![]() ,
,![]() ,…,
,…,![]() ),……(6分)
),……(6分)
所以,![]() ,
,
又 ![]() ,
,
于是![]() ,所以
,所以![]() (
(![]() ,
,![]() ).……(10分)
).……(10分)
(3)由已知,![]() ,
,![]() .……(11分)
.……(11分)
由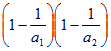 …
…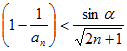 ,得
,得
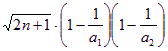 …
…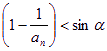 ,
,
令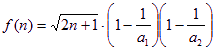 …
…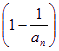 ,则由题意可得
,则由题意可得![]() ,
,
于是
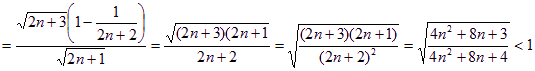 ,
,
所以![]() ,即
,即![]() 随着
随着![]() 的增大而减小.…………(15分)
的增大而减小.…………(15分)
所以当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,
,
若存在角![]() 满足要求,则必须
满足要求,则必须![]() .……(16分)
.……(16分)
所以角![]() 的取值范围为
的取值范围为![]() ,(
,(![]() )…………(18分)
)…………(18分)
(注:说明![]() 单调性的作差方法如下)
单调性的作差方法如下)
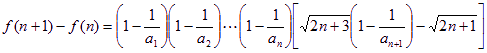
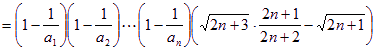
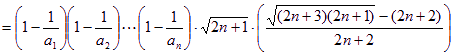
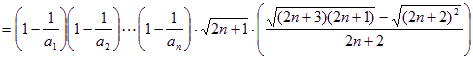
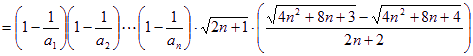 ,
,
因为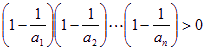 ,
,![]() ,
,![]() ,
,
![]() ,
,
所以![]() ,即
,即![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
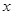 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为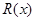 万元,且
万元,且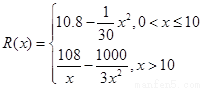 .
.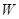 (万元)关于年产量
(万元)关于年产量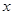 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为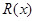 万元,且
万元,且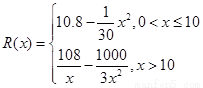 .
. (万元)关于年产量
(万元)关于年产量 、
、 ,点
,点 是直角坐标平面上的动点,若将点
是直角坐标平面上的动点,若将点 的横坐标保持不变、纵坐标扩大到
的横坐标保持不变、纵坐标扩大到 倍后得到点
倍后得到点 满足
满足 .
. 的轨迹方程;
的轨迹方程; 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 两点,且满足
两点,且满足 ,又点
,又点 关于原点O的对称点为点
关于原点O的对称点为点 ,试问四点
,试问四点 是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由. 层,总开发费用为
层,总开发费用为 万元,求函数
万元,求函数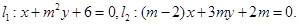 讨论当实数m为何值时,(1)
讨论当实数m为何值时,(1)