题目内容
如图，平面α⊥平面β，α∩β=直线l，A，C是α内不同的两点，B，D是β内不同的两点，且A，B，C，D∉直线l，M，N分别是线段AB，CD的中点．下列判断正确的是②
②
；①．当|CD|=2|AB|时，M，N两点不可能重合
②．M，N两点可能重合，但此时直线AC与l不可能相交
③．当AB与CD相交，直线AC平行于l时，直线BD可以与l相交
④．当AB，CD是异面直线时，直线MN可能与l平行．
分析：根据面面垂直的位置关系，结合直线和点的位置，由位置关系分别判断就可．
解答：解：①当|CD|=2|AB|时，若AC∥BD，
则A，B，C，D四点共面，此时M，N两点能重合．故①错误．
②若M，N两点重合，则AC∥BD，
故AC∥l，此时直线AC与直线l不可能相交，故②正确．
③若AB与CD相交，当直线AC∥l时，直线BD可以与l平行，故③错误．
④若AB，CD是异面直线，
∴根据异面直线的定义可知，MN不可能与l平行，故④错误．
故答案为：②．
则A，B，C，D四点共面，此时M，N两点能重合．故①错误．
②若M，N两点重合，则AC∥BD，
故AC∥l，此时直线AC与直线l不可能相交，故②正确．
③若AB与CD相交，当直线AC∥l时，直线BD可以与l平行，故③错误．
④若AB，CD是异面直线，
∴根据异面直线的定义可知，MN不可能与l平行，故④错误．
故答案为：②．
点评：本题主要考查空间直线位置关系的判断，考查图形的观察能力与运用相关知识证明判断的能力．综合性较强．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知等腰△ABC的底边BC=3，顶角为120°，D是BC边上一点，且BD=1．把△ADC沿AD折起，使得平面CAD⊥平面ABD，连接BC形成三棱锥C-ABD．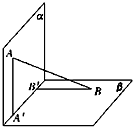
如图，平面α⊥平面β，A∈α，B∈β，AB与平面α、β所成的角分别为
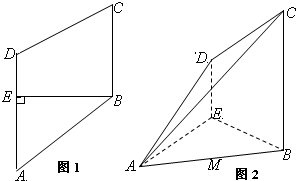（2013•威海二模）如图1，在梯形ABCD中，BC∥DA，BE⊥DA，EA=EB=BC=2，DE=1，将四边形DEBC沿BE折起，使平面DEBC垂直平面ABE，如图2，连结AD，AC．设M是AB上的动点．
如图，平面
平面
，点E、F、O分别为线段PA、PB、AC的中点，点G是线段CO的中点，
，
．
平面
；
∥平面