Question

已知平面上两个定点A、B之间的距离为2a，点M到A、B两点的距离之比为2∶1，求动点M的轨迹方程。

Answer 1

答案：
解析：

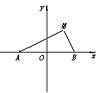
解：如图， 以两定点A、B所在直线为x轴，线段AB的中垂线为y轴建立坐标系 ∵｜AB｜=2A. ∴设A(－a,0),B(a,0),M(x,y) ∵｜MA｜∶｜MB｜=2∶1 ∶ =2∶1 =2 化简，得（x－a)2+y2=a2 ∴所求动点M的轨迹方程为 （x－a）2+y2=a2。