题目内容
数列![]() 的前n项和Sn满足:Sn=2an-3n(nÏN+).
的前n项和Sn满足:Sn=2an-3n(nÏN+).
(1)求数列![]() 的通项公式an;
的通项公式an;
(2)数列![]() 中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
答案:
解析:
解析:
(1)当nÎN+时有:Sn=2an-3n, ∴ Sn+1=2an+1-3(n+1),两式相减得:an+1=2an+1-2an-3 ∴ an+1=2an+3 ∴ an+1+3=2(an+3)又a1=s1=2a1-3, ∴ a1=3,a1+3=6¹0 ∴ 数列 ∴ an=3×2n-3 另解:归纳猜想再用数学归纳法证. (2)假设数列 ∴ ar<as<at,∴ 只能是ar+at=2as, ∴ (3×2r-3)+(3×2t-3)=2(3×2s-3),即2r+2t=2s+1 ∴ 1+2t-r=2s+1-r.(*) ∵ r<s<t,r,s,t均为正整数, ∴ (*)式左边为奇数,右边为偶数,不可能成立. 因此数列
|

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的前n项和为Sn ,且满足
的前n项和为Sn ,且满足 。
。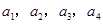 ;
;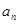 ,并用数学归纳法证明。
,并用数学归纳法证明。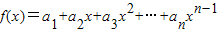 ,
,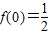 ,数列{an}满
,数列{an}满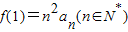 ,则数列{an}的前n项和Sn等于 .
,则数列{an}的前n项和Sn等于 . ,
, ,数列{an}满
,数列{an}满 ,则数列{an}的前n项和Sn等于 .
,则数列{an}的前n项和Sn等于 .