题目内容
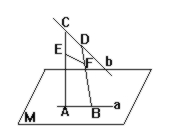
已知a和b是两条异面直线, A和B是a上不同的两点, C和D是b上不同的两点, E、F分别是线段AC和BD的中点. 那么EF和AB, EF和CD的关系是[ ]
A. 两对异面直线. B.三条交于一点的直线.
C.一对平行, 一对异面的直线. D.以上都不对
答案:A
解析:
提示:
解析:
|
解: 如图, 假定直线EF和AB共面, 设此平面为N. 由a和b是异面直线, 知道C与A是不同的点, 因而AC的中点E与A点不重合. 直线AC上有两个不同的点A和E在平面N内,因而直线AC上所有各点都在平面N内C点当然在平面N内,同理D点也在平面N内.直线b上有不同的两点C和D在平面N内, 因而直线b在平面N内. 这样一来, 直线b和a就要在同一平面N内. 而已知a和b是异面直线, 出现矛盾. 所以EF和AB是异面直线. 同理EF和CD是异面直线.
|
提示:
|
用实例观察 |

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
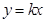 与圆
与圆 恒有公共点;
恒有公共点;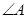 为△ABC的内角,则
为△ABC的内角,则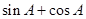 最小值为
最小值为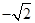 ;
; }中,
}中,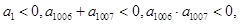 则使其前n项和
则使其前n项和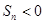 成立的最大正整数为2013;
成立的最大正整数为2013; 与圆
与圆 恒有公共点;
恒有公共点; 为△ABC的内角,则
为△ABC的内角,则 最小值为
最小值为 ;
; }中,
}中, 则使其前n项和
则使其前n项和 成立的最大正整数为2013;
成立的最大正整数为2013; 与圆
与圆 恒有公共点;
恒有公共点; 为△ABC的内角,则
为△ABC的内角,则 最小值为
最小值为 ;
; }中,
}中, 则使其前n项和
则使其前n项和 成立的最大正整数为2013;
成立的最大正整数为2013;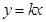 与圆
与圆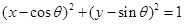 恒有公共点;
恒有公共点;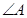 为△ABC的内角,则
为△ABC的内角,则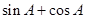 最小值为
最小值为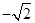 ;
;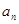 }中,
}中,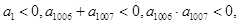 则使其前n项和
则使其前n项和 成立的最大正整数为2013;
成立的最大正整数为2013;