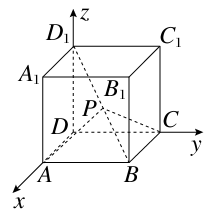
题目内容
如图所示,AO⊥平面α,BC⊥OB,BC与平面α的夹角为30°,AO=BO=BC=a,则AC=______.
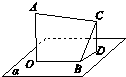

作CD⊥平面α,垂足为D,连接BD,OD,则∠CBD=30°,
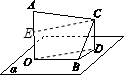
∵BO=BC=a,∴OD=
a,CD=
a
过C作CE⊥AO,垂足为E,则CE=
a,AE=
a
∴AC=
=
a
故答案为:
a

∵BO=BC=a,∴OD=
| ||
| 2 |
| 1 |
| 2 |
过C作CE⊥AO,垂足为E,则CE=
| ||
| 2 |
| 1 |
| 2 |
∴AC=
| CE2+AE2 |
| 2 |
故答案为:
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 中,
中,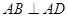 ,
,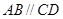 ,
,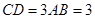 ,平面
,平面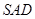 ⊥平面
⊥平面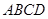 ,
,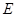 是线段
是线段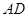 上一点,
上一点,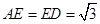 ,
,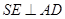 .
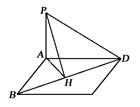
. ⊥平面
⊥平面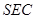 ;
;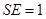 ,求直线
,求直线 与平面
与平面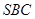 所成角的正弦值.
所成角的正弦值.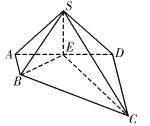
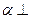 平面
平面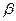 ,
,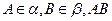 与两平面
与两平面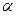 、
、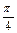 和
和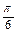 。过A、B分别作两平面交线的垂线,垂足为
。过A、B分别作两平面交线的垂线,垂足为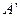 、
、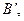 若AB=12,则
若AB=12,则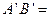
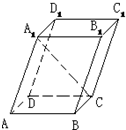
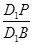 =λ.当∠APC为钝角时,λ的取值范围是________.
=λ.当∠APC为钝角时,λ的取值范围是________.