题目内容
设四棱锥P-ABCD的底面ABCD是单位正方形，PB⊥底面ABCD且PB=
，记∠APD=θ，sinθ=
- A.
- B.
- C.
- D.
B
分析：由几何体的特点，可确定三角形PAD是直角三角形，在直角三角形中先由已知条件求边长，再求sinθ
解答：
解：连接BD
∵PB⊥面ABCD
∴PB⊥BD，PB⊥AD
在△PBD中，PB=，BD=
∴PD=
又∵AB⊥AD，且PB∩AB=B
∴AD⊥面PAB
∴AD⊥PA
∴△PAD是直角三角形
∴sinθ=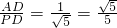
故选B
点评：本题考察线面垂直问题，要熟练掌握线面垂直的判定定理和性质定理，属简单题
分析：由几何体的特点，可确定三角形PAD是直角三角形，在直角三角形中先由已知条件求边长，再求sinθ
解答：
解：连接BD∵PB⊥面ABCD
∴PB⊥BD，PB⊥AD
在△PBD中，PB=
，BD=∴PD=
又∵AB⊥AD，且PB∩AB=B
∴AD⊥面PAB
∴AD⊥PA
∴△PAD是直角三角形
∴sinθ=
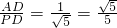
故选B
点评：本题考察线面垂直问题，要熟练掌握线面垂直的判定定理和性质定理，属简单题
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
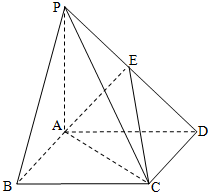设四棱锥P-ABCD中，底面ABCD是边长为2的正方形，且PA⊥面ABCD，PA=AB，E为PD的中点．
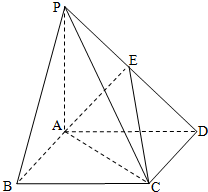设四棱锥P-ABCD中，底面ABCD是边长为2的正方形，且PA⊥面ABCD，PA=AB，E为PD的中点．
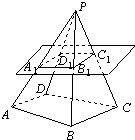设四棱锥P-ABCD的底面不是平行四边形，用平面 α去截此四棱锥，使得截面四边形是平行四边形，则这样的平面α（ ）