题目内容
2.若抛物线x2=ay(a>0)的准线与圆(x-2)2+y2=4相交于A、B两点,且|AB|=2$\sqrt{3}$,则a的值是4.分析 如图所示,抛物线x2=ay(a>0)的准线方程为:y=-$\frac{a}{4}$.取AB的中点D,圆心为C,连接CD.可得|AD|=$\frac{1}{2}$|AB|=$\sqrt{3}$,|AC|=2,利用|CD|=$\sqrt{|AC{|}^{2}-|AD{|}^{2}}$=$\frac{a}{4}$,即可解出.
解答 解:如图所示,
抛物线x2=ay(a>0)的准线方程为:y=-$\frac{a}{4}$.
取AB的中点D,圆心为C,连接CD.
则|AD|=$\frac{1}{2}$|AB|=$\sqrt{3}$,|AC|=2,
∴|CD|=$\sqrt{|AC{|}^{2}-|AD{|}^{2}}$=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}$=1,
∴$\frac{a}{4}$=1,
解得a=4.
故答案为:4.
点评 本题考查了抛物线与圆的标准方程及其性质、垂经定理、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.过抛物线y2=2px(p>0)的焦点F的直线l,依次分别交抛物线的准线、y轴、抛物线于A、B、C三点.若$\overrightarrow{{A}{B}}=2\overrightarrow{{B}C}$,则直线l的斜率是( )
| A. | $-\sqrt{2}$或$\sqrt{2}$ | B. | -2或2 | C. | $-2\sqrt{2}$或$2\sqrt{2}$ | D. | -4或4 |
14.点P在抛物线y2=8x上,点Q在圆(x-6)2+y2=1上,则|PQ|的最小值为( )
| A. | 5 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 4$\sqrt{2}$-1 |
11.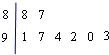 若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,
若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,
叶为个位数,则这组数据的中位数和平均数分别是( )
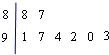 若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,
若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,叶为个位数,则这组数据的中位数和平均数分别是( )
| A. | 91,91.5 | B. | 91,92 | C. | 91.5,91.5 | D. | 91.5,92 |
 的终边过点
的终边过点 ,则
,则 等于( )
等于( ) B.
B.
 D.5
D.5 的图象和函数
的图象和函数 的图象的交点个数是( )
的图象的交点个数是( ) 是三个全等的菱形,
是三个全等的菱形, ,设
,设 .已知点
.已知点 在各菱形边上运动,且
在各菱形边上运动,且 的最大值为( )
的最大值为( )
 中,
中, 且
且 ,则
,则 ( )
( ) B.3
B.3  D.7
D.7