题目内容
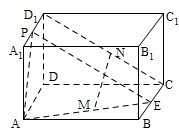 如图,长方体ABCD-A1B1C1D1中,E、P分别是BC、A1D1的中点,M、N分别是AE、CD1的中点,AD=AA1=a,AB=2a,
如图,长方体ABCD-A1B1C1D1中,E、P分别是BC、A1D1的中点,M、N分别是AE、CD1的中点,AD=AA1=a,AB=2a,(Ⅰ)求证:MN∥平面ADD1A1;
(Ⅱ)求二面角P-AE-D的大小;
(Ⅲ)求三棱锥P-DEN的体积.
分析:法一、(1)要证明线面平行,关键是在平面内找到一条可能与已知直线平行的直线,观察到平面ADD1A1中三条已知直线与PC都不平行,故我们要考虑在平面ADD1A1中做一条与PC可能平行直线辅助线,然后再进行证明.
(2)要求二面角的余弦,要先构造出二面角的平面角,然后利用解三角形的方法,求出这个平面角的余弦值,进而给出二面角的余弦值.
(3)要求三棱锥的体积,只要求出底面的面积,及对应的高代入棱锥体积公式,即可求解.
法二、构造空间直角坐标系,求出各点的坐标,进行求出相应直线的方向向量和平面的法向量,利用向量法进行求解.
(2)要求二面角的余弦,要先构造出二面角的平面角,然后利用解三角形的方法,求出这个平面角的余弦值,进而给出二面角的余弦值.
(3)要求三棱锥的体积,只要求出底面的面积,及对应的高代入棱锥体积公式,即可求解.
法二、构造空间直角坐标系,求出各点的坐标,进行求出相应直线的方向向量和平面的法向量,利用向量法进行求解.
解答: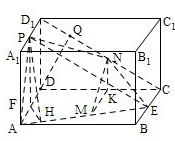 解:法一:(Ⅰ)证明:取CD的中点K,连接MK,NK
解:法一:(Ⅰ)证明:取CD的中点K,连接MK,NK
∵M,N,K分别为AK,CD1,CD的中点
∵MK∥AD,NK∥DD1
∴MK∥面ADD1A1,NK∥面ADD1A1,又MK与NK交于K
∴面MNK∥面ADD1A1,
∴MN∥面ADD1A1
(Ⅱ)设F为AD的中点
∵P为A1D1的中点∴PF∥D1D∴PF⊥面ABCD
作FH⊥AE,交AE于H,连接PH,则由三垂线定理得AE⊥PH
从而∠PHF为二面角P-AE-D的平面角.
在Rt△AEF中,AF=
,EF=2a,AE=
a,
从而FH=
=
=
在Rt△PFH中,tan∠PFH=
=
=
故:二面角P-AE-D的大小为arctan
(Ⅲ)S△NEP=
S矩形ECD1P=
BC•CD1=
•a•
=
a2
作DQ⊥CD1,交CD1于Q,由A1D1⊥面CDD1C1得A1C1⊥DQ
∴DQ⊥面BCD1A1
∴在Rt△CDD1中,DQ=
=
=
a
∴VP-DEN=VD-ENP=
S△NEP•DQ=
a2•
a=
a3
方法二:以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立直角坐标系,

则A(a,0,0),B(a,2a,0),C(0,2a,0),A1(a,0,a),D1(0,0,a)
∵E,P,M,N分别是BC,A1D1,AE,CD1的中点
∴E(
,2a,0),P(
,0,a),M(
,a,0),N(0,a,
),
(Ⅰ)
=(-
a,0,
)
取
=(0,1,0),显然
⊥面ADD1A1
•
=0,
∴
⊥
又MN∉面ADD1A1
∴MN∥面ADD1A1
(Ⅱ)过P作PH⊥AE,交AE于H,取AD的中点F,则F(
,0,0)
∵设H(x,y,0),则
=(
-x,-y,a),
=(
-x,-y,0)
又
=(-
,2a,0)
由
•
=0,及H在直线AE上,可得:
解得x=
a,y=
a
∴
=(-
,-
,a),
=(-
,-
,0)
∴
•
=0即
⊥
∴
与
所夹的角等于二面角P-AE-D的大小cos?
,
>=
=
故:二面角P-AE-D的大小为arccos
(Ⅲ)设
=(x1,y1,z1)为平面DEN的法向量,
则
⊥
,
⊥
又
=(
,2a,0),
=(0,a,
),
=(
,0,a)
∴
即
∴可取
=(4,-1,2)
∴P点到平面DEN的距离为d=
=
=
∵cos?
,
>=
=
,sin?
,
>=
∴S△DEN=
|
|•|
|•sin?
,
>=
a2
∴VP-DEN=
S△DEN•d=
×
a2×
=
 解:法一:(Ⅰ)证明:取CD的中点K,连接MK,NK
解:法一:(Ⅰ)证明:取CD的中点K,连接MK,NK∵M,N,K分别为AK,CD1,CD的中点
∵MK∥AD,NK∥DD1
∴MK∥面ADD1A1,NK∥面ADD1A1,又MK与NK交于K
∴面MNK∥面ADD1A1,
∴MN∥面ADD1A1
(Ⅱ)设F为AD的中点
∵P为A1D1的中点∴PF∥D1D∴PF⊥面ABCD
作FH⊥AE,交AE于H,连接PH,则由三垂线定理得AE⊥PH
从而∠PHF为二面角P-AE-D的平面角.
在Rt△AEF中,AF=
| a |
| 2 |
| ||
| 2 |
从而FH=
| AF•EF |
| AE |
| ||||
|
| 2a | ||
|
在Rt△PFH中,tan∠PFH=
| PF |
| FH |
| DD1 |
| FH |
| ||
| 2 |
故:二面角P-AE-D的大小为arctan
| ||
| 2 |
(Ⅲ)S△NEP=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| a2+4a2 |
| ||
| 4 |
作DQ⊥CD1,交CD1于Q,由A1D1⊥面CDD1C1得A1C1⊥DQ
∴DQ⊥面BCD1A1
∴在Rt△CDD1中,DQ=
| CD•DD1 |
| CD1 |
| 2a•a | ||
|
| 2 | ||
|
∴VP-DEN=VD-ENP=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 2 | ||
|
| 1 |
| 6 |
方法二:以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立直角坐标系,

则A(a,0,0),B(a,2a,0),C(0,2a,0),A1(a,0,a),D1(0,0,a)
∵E,P,M,N分别是BC,A1D1,AE,CD1的中点
∴E(
| a |
| 2 |
| a |
| 2 |
| 3a |
| 4 |
| a |
| 2 |
(Ⅰ)
| MN |
| 3 |
| 4 |
| a |
| 2 |
取
| n |
| n |
| MN |
| n |
∴
| MN |
| n |
又MN∉面ADD1A1
∴MN∥面ADD1A1
(Ⅱ)过P作PH⊥AE,交AE于H,取AD的中点F,则F(
| a |
| 2 |
∵设H(x,y,0),则
| HP |
| a |
| 2 |
| HF |
| a |
| 2 |
又
| AE |
| a |
| 2 |
由
| AP |
| AE |
|
解得x=
| 33 |
| 34 |
| 2 |
| 17 |
∴
| HP |
| 8a |
| 17 |
| 2a |
| 17 |
| HF |
| 8a |
| 17 |
| 2a |
| 17 |
∴
| HF |
| AE |
| HF |
| AE |
∴
| HP |
| HF |
| HP |
| HF |
| ||||
|
|
| 2 | ||
|
故:二面角P-AE-D的大小为arccos
2
| ||
| 21 |
(Ⅲ)设
| n1 |
则
| n1 |
| DE |
| n1 |
| DN |
又
| DE |
| a |
| 2 |
| DN |
| a |
| 2 |
| DP |
| a |
| 2 |
∴
|
|
| n1 |
∴P点到平面DEN的距离为d=
|
| ||||
|
|
| |2a+2a| | ||
|
| 4a | ||
|
∵cos?
| DE |
| DN |
| ||||
|
|
| 8 | ||
|
| DE |
| DN |
| ||
|
∴S△DEN=
| 1 |
| 2 |
| DE |
| DN |
| DE |
| DN |
| ||
| 8 |
∴VP-DEN=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 8 |
| 4a | ||
|
| a3 |
| 6 |
点评:判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a?α,b?α,a∥b?a∥α);③利用面面平行的性质定理(α∥β,a?α?a∥β);④利用面面平行的性质(α∥β,a?α,a?,a∥α??a∥β).
求二面角,关键是构造出二面角的平面角,常用的方法有利用三垂线定理和通过求法向量的夹角,然后再将其转化为二面角的平面角.本题也可以用空间向量来解决,其步骤是:建立空间直角坐标系?明确相关点的坐标?明确相关向量的坐标?通过空间向量的坐标运算求解.
求二面角,关键是构造出二面角的平面角,常用的方法有利用三垂线定理和通过求法向量的夹角,然后再将其转化为二面角的平面角.本题也可以用空间向量来解决,其步骤是:建立空间直角坐标系?明确相关点的坐标?明确相关向量的坐标?通过空间向量的坐标运算求解.

练习册系列答案
相关题目
 19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 15、如图,长方体ABCD-A1B1C1D1中被截去一部分,
15、如图,长方体ABCD-A1B1C1D1中被截去一部分, 如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中
如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中 如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.
如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.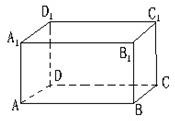 已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )
已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )