题目内容
△ABC中，∠ABC=60°，AC=12，BC=k，若满足条件的三角形恰有一个，则k的取之集合为 ．
分析：利用正弦定理列出关系式，将各自的值代入表示出k，根据A的范围求出sinA的范围，即可确定出k的范围．
解答：解：∵△ABC中，∠ABC=60°，AC=12，BC=k，
∴由正弦定理
=
=
得：
=
，即k=8
sinA，
∵0＜A＜120°，∴0＜sinA≤1，
则k的取值范围为（0，8
]．
故答案为：（0，8
]
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| 12 |
| sin60° |
| k |
| sinA |
| 3 |
∵0＜A＜120°，∴0＜sinA≤1，
则k的取值范围为（0，8
| 3 |
故答案为：（0，8
| 3 |
点评：此题考查了正弦定理，以及正弦函数的定义域与值域，熟练掌握正弦定理是解本题的关键．
练习册系列答案
相关题目
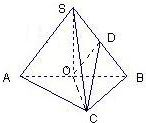
在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2