题目内容
18.函数y=$\frac{1}{\sqrt{sin2x}}$的定义域为(kπ,kπ+$\frac{π}{2}$)(k∈Z).分析 由分母中根式内部的代数式大于0,求解三角不等式得答案.
解答 解:由sin2x>0,得2kπ<2x<π+2kπ,即$kπ<x<\frac{π}{2}+kπ,k∈Z$.
∴函数y=$\frac{1}{\sqrt{sin2x}}$的定义域为(kπ,kπ+$\frac{π}{2}$)(k∈Z).
故答案为:(kπ,kπ+$\frac{π}{2}$)(k∈Z).
点评 本题考查函数的定义域及其求法,考查了三角不等式的解法,是基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
6.已知幂函数f(x)=(m-1)xa的图象过点(9,3),数列{an}各项均为正值,且a1=$\frac{m}{2}$,a2=m,且$\frac{{a}_{n}}{{a}_{n-1}}$=f($\frac{{a}_{n+1}}{{a}_{n}}$)(n>1),则a10=( )
| A. | 210 | B. | 245 | C. | 288 | D. | 2511 |
8.已知点P为△ABC所在平面内一点,|$\overrightarrow{CA}$|=|$\overrightarrow{CB}$|=1且$\overrightarrow{CP}$=$\overrightarrow{CA}$+$\overrightarrow{CB}$,则点P在( )
| A. | △ABC内心上 | B. | 直线AB上 | C. | △ABC垂心上 | D. | ∠ACB的平分线上 |
 已知函数f(x)=|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|.
已知函数f(x)=|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|. 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为3的等腰三角形.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为3的等腰三角形.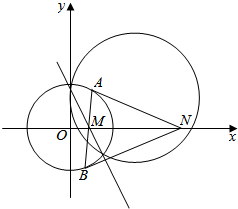 已知圆O:x2+y2=4和圆C:x2+y2-2x-y-2=0,记两圆的公共弦所在的直线为l.
已知圆O:x2+y2=4和圆C:x2+y2-2x-y-2=0,记两圆的公共弦所在的直线为l.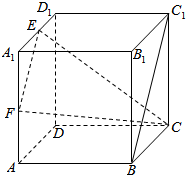 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1A的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1A的中点.