题目内容
设集合A={(x,y)|y=
},B={(x,y)|y=k(x+2)-1},且A∩B≠∅,则实数k的取值范围是______.
| 1-x2 |
集合A中的函数表示圆心为原点,半径为1的上半圆,集合B中的函数表示恒过(-2,-1)的直线,
当过M与半圆相切,切点在第二象限时,圆心O到直线的距离d=r,即
=1,
整理得:4k2-4k+1=1+k2,即3k2-4k=0,即k(3k-4)=0,
解得:k=0(舍去)或k=
,
当直线过(1,0)时,将x=1,y=0代入直线方程得:0=3k-1,即k=
,
∵A∩B≠∅,∴两函数有交点,
则实数k的取值范围是[
,
].
故答案为:[
,
]

当过M与半圆相切,切点在第二象限时,圆心O到直线的距离d=r,即
| |2k-1| | ||
|
整理得:4k2-4k+1=1+k2,即3k2-4k=0,即k(3k-4)=0,
解得:k=0(舍去)或k=
| 4 |
| 3 |
当直线过(1,0)时,将x=1,y=0代入直线方程得:0=3k-1,即k=
| 1 |
| 3 |
∵A∩B≠∅,∴两函数有交点,
则实数k的取值范围是[
| 1 |
| 3 |
| 4 |
| 3 |
故答案为:[
| 1 |
| 3 |
| 4 |
| 3 |


练习册系列答案
相关题目
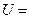
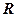 ,
,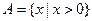 ,
,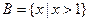 ,则
,则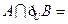
 ( )
( )