题目内容
已知椭圆的标准方程为 ,且c=1,如果直线:3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点,
,且c=1,如果直线:3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点,
(1)求椭圆的标准方程;
(2)设直线与椭圆在第一象限内的交点为P,F是椭圆的右焦点,若直线4x+3y+m=0与以PF为直径的圆相切,求实数m的值;
(3)设M是椭圆上任意一点,F是椭圆的一个焦点,试探究以椭圆长轴为直径的圆O与以MF为直径的圆的位置关系。
 ,且c=1,如果直线:3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点,
,且c=1,如果直线:3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点,(1)求椭圆的标准方程;
(2)设直线与椭圆在第一象限内的交点为P,F是椭圆的右焦点,若直线4x+3y+m=0与以PF为直径的圆相切,求实数m的值;
(3)设M是椭圆上任意一点,F是椭圆的一个焦点,试探究以椭圆长轴为直径的圆O与以MF为直径的圆的位置关系。
解:(1)直线3x-2y=0 与椭圆的一个交点的坐标为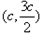 ,
,
代入椭圆方程得: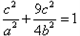 ,
,
又c=1,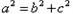 ,
,
解得:a=2,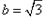 ,
,
所以,椭圆的标准方程为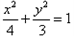 。
。
(2)由(1)知 ,F(1,0),
,F(1,0),
则以PF为直径的圆的方程为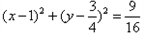 ,
,
圆心坐标为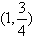 ,半径为
,半径为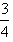 ;
;
当直线4x+3y+m=0与圆相切时,
则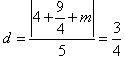 ,解得m=-10或
,解得m=-10或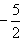 ;
;
(3)设F′是椭圆的另一个焦点,则有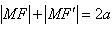 ,
,
以MF为直径的圆的圆心为N,半径为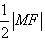 ,
,
又圆O的半径为a,
所以两圆圆心之间的距离是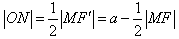 ,故两圆内切。
,故两圆内切。
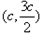 ,
,代入椭圆方程得:
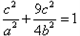 ,
, 又c=1,
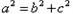 ,
,解得:a=2,
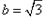 ,
, 所以,椭圆的标准方程为
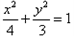 。
。(2)由(1)知
 ,F(1,0),
,F(1,0),则以PF为直径的圆的方程为
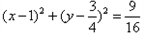 ,
, 圆心坐标为
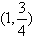 ,半径为
,半径为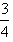 ;
;当直线4x+3y+m=0与圆相切时,
则
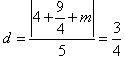 ,解得m=-10或
,解得m=-10或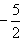 ;
; (3)设F′是椭圆的另一个焦点,则有
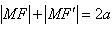 ,
,以MF为直径的圆的圆心为N,半径为
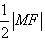 ,
,又圆O的半径为a,
所以两圆圆心之间的距离是
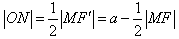 ,故两圆内切。
,故两圆内切。
练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 ,则椭圆的离心率为(
)
,则椭圆的离心率为(
) B、
B、 C、
C、 D、
D、