题目内容
设zn=(
)n,n∈N*,则数列{|zn+1-zn|}的所有项的和为S= .
| 1+i |
| 2 |
考点:数列的求和,复数代数形式的乘除运算
专题:等差数列与等比数列,数系的扩充和复数
分析:首先利用复数的运算求出数列的通项公式进一步利用极限求和.
解答:
解:由于:Zn=(
)n
所以:Zn+1=(
)n+1
|Zn+1-Zn|=|(
)n+1-(
)n|=(
)n+1
所以:
Sn=
=
| 1+i |
| 2 |
所以:Zn+1=(
| 1+i |
| 2 |
|Zn+1-Zn|=|(
| 1+i |
| 2 |
| 1+i |
| 2 |
| ||
| 2 |
所以:
| lim |
| n→∞ |
| ||||||
1-
|
2+
| ||
| 2 |
点评:本题考查的知识要点:复数的运算问题,数列的通项公式的应用.属于基础题型.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
设A={x∈N|1≤x<6},则下列正确的是( )
| A、6∈A | B、0∈A |
| C、3?A | D、3.5∉a |
在△ABC中,D是BC边上的一点,
=λ(
+
).|
|=2,|
=4,若记
=
,
=
,则用
,
表示
所得的结果为( )
| AD |
| ||
|
|
| ||
|
|
| AB |
| AC| |
| AB |
| a |
| AC |
| b |
| a |
| b |
| BD |
A、
| ||||||||
B、
| ||||||||
C、-
| ||||||||
D、
|
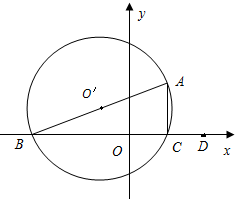 如图,在平面直角坐标系中,△ABC内接于⊙O,其中AB为⊙O直径,A(1,3),B(-3,0),C(1,0).
如图,在平面直角坐标系中,△ABC内接于⊙O,其中AB为⊙O直径,A(1,3),B(-3,0),C(1,0).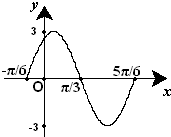 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的一段图象(如图)所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的一段图象(如图)所示.