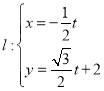题目内容
【题目】已知椭圆![]() :
:![]() 的上顶点为
的上顶点为![]() ,左,右焦点分别为
,左,右焦点分别为![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
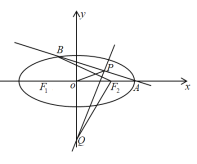
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 的面积为
的面积为![]() 可得,
可得,![]() ,由直线
,由直线![]() 的斜率为
的斜率为![]() ,有
,有![]() ,再根据
,再根据![]() ,可解得
,可解得![]() 的值,得到椭圆方程.
的值,得到椭圆方程.
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,将直线
,将直线![]() 的方程与椭圆方程联立解出点
的方程与椭圆方程联立解出点![]() 坐标,由
坐标,由![]() ,得出点
,得出点![]() 坐标,再由
坐标,再由![]() ,得
,得![]() 为
为![]() 的垂直平分线与
的垂直平分线与![]() 的交点,所以
的交点,所以![]() ,根据由
,根据由![]() 得出斜率
得出斜率![]() 的值,从而得出直线方程.
的值,从而得出直线方程.
(1)因为![]() 的面积为
的面积为![]() ,所以
,所以![]()
由直线![]() 的斜率为
的斜率为![]() ,则
,则![]() ,又
,又![]() ,
,
所以![]() ,
,![]() ,故椭圆方程为
,故椭圆方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
由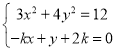 ,可得
,可得![]() ,
,
解得![]() 或
或![]() ,所以
,所以![]() ,
,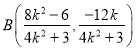 ,
,
设![]() ,有
,有![]() ,
,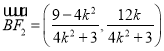 ,
,
由![]() ,得
,得![]() ,
,
所以![]() ,解得
,解得![]() ,
,
由![]() ,得
,得![]() 为
为![]() 的垂直平分线与
的垂直平分线与![]() 的交点,所以
的交点,所以![]() ,
,
由![]() ,得
,得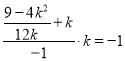 ,
,
得![]() ,解得
,解得![]() ,
,
所以,直线![]() 的方程为
的方程为![]() .
.

【题目】为提倡节能减排,同时减轻居民负担,广州市积极推进“一户一表”工程![]() 非一户一表用户电费采用“合表电价”收费标准:
非一户一表用户电费采用“合表电价”收费标准:![]() 元
元![]() 度
度![]() “一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执行非夏季标准如下:
“一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执行非夏季标准如下:
第一档 | 第二档 | 第三档 | |
每户每月用电量 |
|
|
|
电价 |
|
|
|
例如:某用户11月用电410度,采用合表电价收费标准,应交电费![]() 元,若采用阶梯电价收费标准,应交电费
元,若采用阶梯电价收费标准,应交电费![]() 元.
元.
为调查阶梯电价是否能到“减轻居民负担”的效果,随机调查了该市100户的11月用电量,工作人员已经将90户的月用电量填在下面的频率分布表中,最后10户的月用电量![]() 单位:度
单位:度![]() 为:88、268、370、140、440、420、520、320、230、380.
为:88、268、370、140、440、420、520、320、230、380.

(1)在答题卡中完成频率分布表,并绘制频率分布直方图;

![]() 根据已有信息,试估计全市住户11月的平均用电量
根据已有信息,试估计全市住户11月的平均用电量![]() 同一组数据用该区间的中点值作代表
同一组数据用该区间的中点值作代表![]() ;
;
![]() 设某用户11月用电量为x度
设某用户11月用电量为x度![]() ,按照合表电价收费标准应交
,按照合表电价收费标准应交![]() 元,按照阶梯电价收费标准应交
元,按照阶梯电价收费标准应交![]() 元,请用x表示
元,请用x表示![]() 和
和![]() ,并求当
,并求当![]() 时,x的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于
时,x的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于![]() 的用户带来实惠?
的用户带来实惠?