题目内容
若曲线y=
与直线y=x+b有一个公共点,则b的取值范围是
≤b<
≤b<
.
| 3-x2 |
b=
或-
≤b≤
| 6 |
| 3 |
| 3 |
b=
或-
≤b≤
;若有两个交点,则b的取值范围是| 6 |
| 3 |
| 3 |
| 3 |
| 6 |
| 3 |
| 6 |
分析:将曲线y=
平方整理,得它以原点O为圆心,半径为
的圆的上半圆.而直线y=x+b是与y=x平行或重合的一条直线,将直线y=x+b进行平移并观察两图象公共点的个数,则不难得到本题的答案.
| 3-x2 |
| 3 |
解答:解: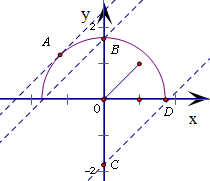 将曲线y=
将曲线y=
两边平方,得
x2+y2=3,(y≥0)
∴曲线y=
表示以原点O为圆心,半径为
的圆的上半圆(含端点)
而直线y=x+b是与y=x平行或重合的一条直线,将直线y=x+b进行平移,得
①当直线y=x+b与半圆相切于点A(-
,
),
或直线y=x+b经过y轴上点B(0,
)与C(0,-
)或线段BC上一点时,
直线与半圆有且仅有一个公共点,此时b=
或-
≤b≤
;
②当直线y=x+b经过点B,或直线y=x+b位于点A、B之间时,
直线与半圆有两个公共点,此时
≤b<
故答案为:b=
或-
≤b≤
,
≤b<
 将曲线y=
将曲线y=| 3-x2 |
x2+y2=3,(y≥0)
∴曲线y=
| 3-x2 |
| 3 |
而直线y=x+b是与y=x平行或重合的一条直线,将直线y=x+b进行平移,得
①当直线y=x+b与半圆相切于点A(-
| ||
| 2 |
| ||
| 2 |
或直线y=x+b经过y轴上点B(0,
| 3 |
| 3 |
直线与半圆有且仅有一个公共点,此时b=
| 6 |
| 3 |
| 3 |
②当直线y=x+b经过点B,或直线y=x+b位于点A、B之间时,
直线与半圆有两个公共点,此时
| 3 |
| 6 |
故答案为:b=
| 6 |
| 3 |
| 3 |
| 3 |
| 6 |
点评:本题给出半圆与动直线,要我们探索它们公共点的个数并加以计算,着重考查了曲线方程的化简、直线与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
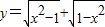 是偶函数,但不是奇函数.
是偶函数,但不是奇函数.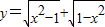 是偶函数,但不是奇函数.
是偶函数,但不是奇函数.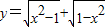 是偶函数,但不是奇函数.
是偶函数,但不是奇函数.