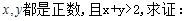题目内容
已知 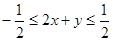 ,
,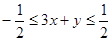 ,求
,求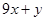 的取值范围。
的取值范围。
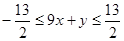
解析试题分析:错解: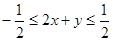 ……(1),
……(1), 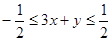 ……(2)
……(2)
(1)×(-1)+(2) 得  ,故
,故 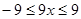 ,
,
(1)×3+(2)×(-2) 得 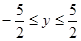 ,
,
以上两不等式相加,得 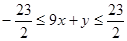 .
.
正解1:设 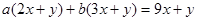 , 比较两边系数得
, 比较两边系数得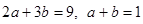
以上两式联立解得 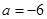 ,
,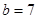
由已知不等式得 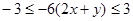 ,
,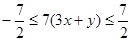 ,
,
以上两不等式相加,得 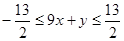 .
.
正解2: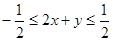 ……(1),
……(1), 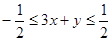 ……(2)
……(2)
(1)×(-1)+(2) 得  ,故
,故 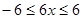 ……(3),
……(3),
(2)+(3) 得 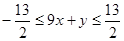 .
.
考点:不等式的求解
点评:利用不等式的可加性来求解不等式的取值范围,属于基础题。

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
不等式x(2﹣x)≤0的解集为( )
| A.{x|0≤x≤2} | B.{x|x≤0,或x≥2} | C.{x|x≤2} | D.{x|x≥0} |
下列不等式的解集是空集的是( )
A. | B. |
C.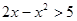 | D. |
已知 ,则“
,则“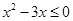 ”是“
”是“ 成立”的( )
成立”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
不等式 的解集是( )
的解集是( )
A.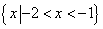 |
B. |
C.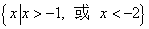 |
D. |
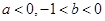 ,则
,则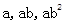 三者的从小到大的关系为__________;
三者的从小到大的关系为__________; 的一个近似值,令
的一个近似值,令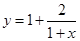 .
. ;
;